高一数学人教A版必修1课件：1.1.3 集合的基本运算（1） .pptVIP免费

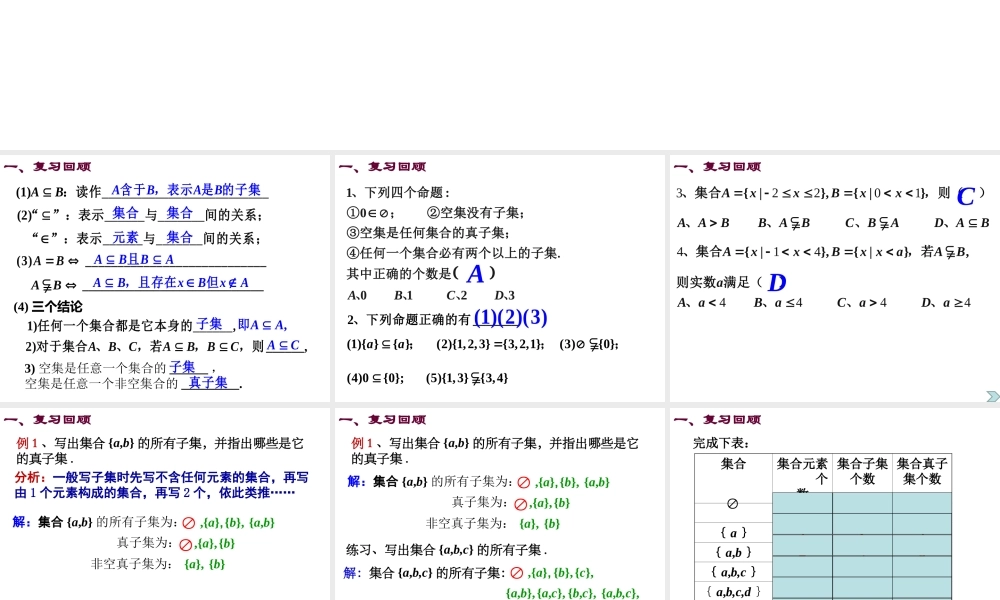
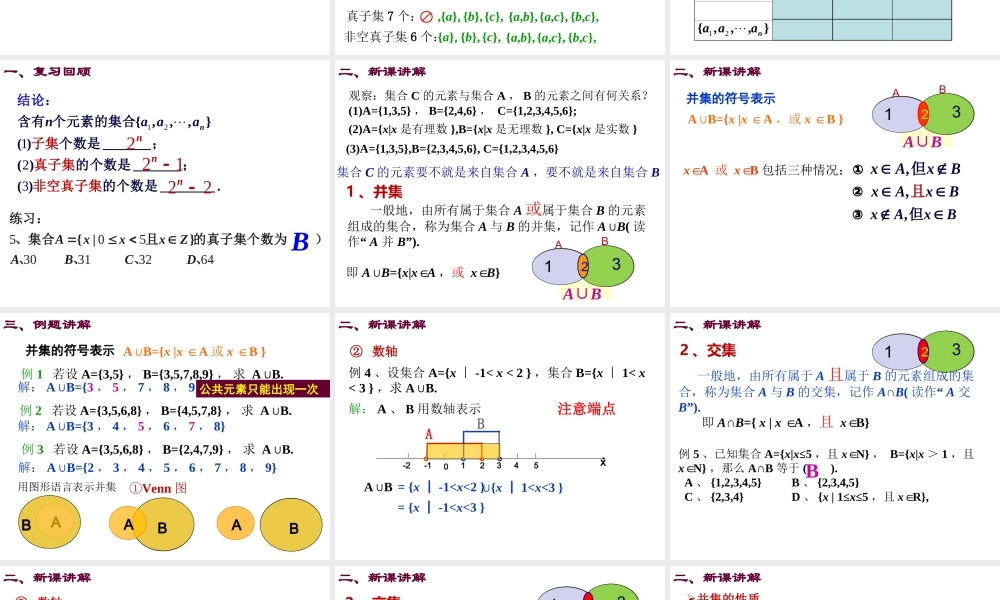
1.1.3集合的基本运算（1）一、复习回顾(1)AB：读作_________________________ABAB含于，表示是的子集(2)“”：表示______与_______间的关系；“”：表示______与_______间的关系；集合集合元素集合(3)____________________________ABABBA且____________________________ABABxBxA，且存在但(4)三个结论3)空集是任意一个集合的______，空集是任意一个非空集合的_________.1)任何一个集合都是它本身的______,2)______,ABCABBC对于集合、、，若，，则子集,AA即AC子集真子集一、复习回顾1:00123ABCD、下列四个命题①；②空集没有子集；③空集是任何集合的真子集；④任何一个集合必有两个以上的子集.其中正确的个数是、、、、A2_______(1){}{}(2){1,2,3}{3,2,1}(3){0}(4)0{0};(5){1,3}{3,4}aa、下列命题正确的有；；；(1)(2)(3)32201{|},{|}AxxBxxAABBABCBADAB、集合，则（）、、、、一、复习回顾4144444{|},{|},AxxBxxaABaAaBaCaDa、集合，若则实数满足（）、、、、CD一、复习回顾例1、写出集合{a,b}的所有子集，并指出哪些是它的真子集.分析：一般写子集时先写不含任何元素的集合，再写由1个元素构成的集合，再写2个，依此类推……解：集合{a,b}的所有子集为：{a,b}真子集为：,{a},{b}非空真子集为：{a},{b},{a},{b},一、复习回顾例1、写出集合{a,b}的所有子集，并指出哪些是它的真子集.解：集合{a,b}的所有子集为：{a,b}真子集为：,{a},{b}非空真子集为：{a},{b},{a},{b},练习、写出集合{a,b,c}的所有子集.解：集合{a,b,c}的所有子集：,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c},真子集7个：,{a},{b},{c},{a,b},{a,c},{b,c},非空真子集6个：{a},{b},{c},{a,b},{a,c},{b,c},一、复习回顾完成下表：集合集合元素个数集合子集个数集合真子集个数010｛a｝121｛a,b｝243｛a,b,c｝387｛a,b,c,d｝41615………n个元素2n2n-112{,,,}naaa12123{,,,}()_______()_______()________.nnaaa含有个元素的集合个数是；的个数是；的个子集真子结集非空真子集数是论：2n21n22n一、复习回顾50530313264{|}AxxxZABCD练习：、集合且的真子集个数为（）、、、、B一般地，由所有属于集合A或属于集合B的元素组成的集合，称为集合A与B的并集，记作A∪B(读“作A并B”).即A∪B={x|x∈A，或x∈B}A∪BAB观察：集合C的元素与集合A，B的元...