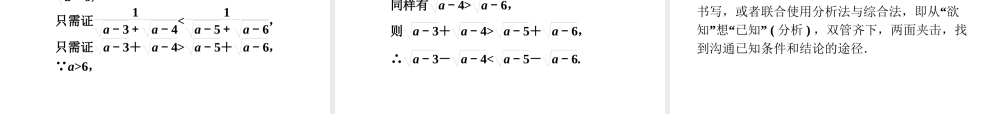2.2直接证明与间接证明2.2.1综合法与分析法学习目标1.了解直接证明的两种基本方法——综合法和分析法.2.理解综合法和分析法的思考过程、特点,会用综合法和分析法证明数学问题.课前自主学案1.合情推理包括____推理和____推理;演绎推理的“三段论”包括______、______和____.2.“a>b>0”是a2>b2的__________条件.温故夯基3.因为a+b≥2ab(a>0,b>0),所以x+1x≥2(x>0),且当x=_,x+1x(x>0)取最小值_.归纳类比大前提小前提结论充分不必要12综合法和分析法知新益能综合法分析法定义利用________和某些数学_____、_____、_____等,经过一系列的__________,最后推导出所要证明的结论成立,这种证明方法叫做综合法从要证明的_________,逐步寻求使它成立的_________,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、____、____、____等),这种证明方法叫做分析法框图表示P⇒Q1→Q1⇒Q2→Q2⇒Q3→…→Qn⇒Q(P表示________、已有的____、____、____等,Q表示______________Q⇐P1→P1⇐P2→P2⇐P3→…→得到一个明显成立的条件特点顺推证法或由因导果法逆推证法或执果索因法已知条件定义公理定理推理论证结论出发充分条件定理定义公理所要证明的结论已知条件定义公理定理1.综合法与分析法的推理过程是合情推理还是演绎推理?提示:综合法与分析法的推理过程是演绎推理,因为综合法与分析法的每一步推理都是严密的逻辑推理,从而得到的每一个结论都是正确的,不同于合情推理中的“猜想”.问题探究2.分析法是把所要求证的结论当作已知条件来推理吗?提示:分析法并不是把所要求证的结论当作已知条件来推理,而是寻求使结论成立的充分条件.课堂互动讲练综合法的应用综合法的思维特点是:从“已知”看“可知”,逐步推向“未知”,其逐步推理实际上是寻找它的必要条件.考点突破已知a、b是正数,且a+b=1,求证:1a+1b≥4.例1【思路点拨】解答本题可由已知条件出发,结合基本不等式,即可得出结论.【证明】法一: a,b是正数且a+b=1,∴a+b≥2ab,当且仅当a=b时,取“=”号,∴ab≤12,∴ab≤14,∴1a+1b=a+bab=1ab≥4.法二: a,b是正数,∴a+b≥2ab>0,1a+1b≥21ab>0,当且仅当a=b时,取“=”号,∴(a+b)(1a+1b)≥4.又a+b=1,∴1a+1b≥4.法三:1a+1b=a+ba+a+bb=1+ba+ab+1≥2+2ba·ab=4,当且仅当a=b时,取“=”号.【思维总结】综合法证明不等式所依赖的主要是不等式的基本性质和...