正弦、余弦函数的性质1.pptVIP免费

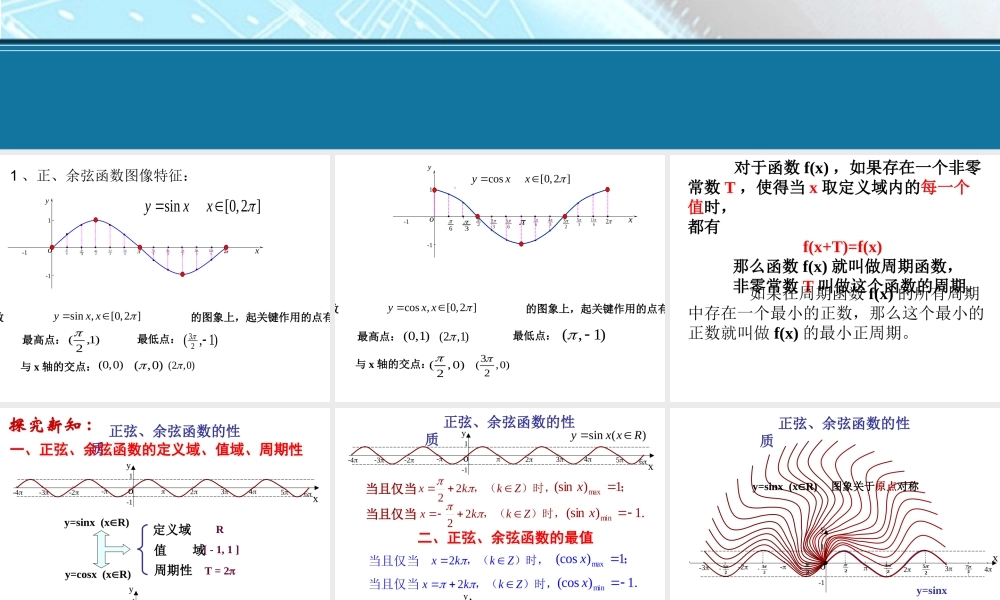
正弦、余弦函数的性质(1)1、正、余弦函数图像特征：2oxy---11--13232656734233561126sin[0,2]yxx数的图象上，起关键作用的点有sin,[0,2]yxx最高点：最低点：与x轴的交点：(0,0)(,0)(2,0))1,(23)1,2(-oxy---11--13232656734233561126cos[0,2]yxx数的图象上，起关键作用的点有cos,[0,2]yxx最高点：最低点：与x轴的交点：(0,1)3(,0)2(2,1)(,1)(,0)2对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x+T)=f(x)那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期。如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小的正数就叫做f(x)的最小正周期。正弦、余弦函数的性质x6yo--12345-2-3-41y=sinx(xR)x6o--12345-2-3-41yy=cosx(xR)定义域值域周期性R[-1,1]T=2探究新知:一、正弦、余弦函数的定义域、值域、周期性正弦、余弦函数的性质x6yo--12345-2-3-41x6o--12345-2-3-41y当且仅当）时，，（Zkkx22；1)(sinmaxx当且仅当）时，，（Zkkx22.1)(sinminx当且仅当）时，，（Zkkx2；1)(cosmaxx当且仅当）时，，（Zkkx2.1)(cosminx二、正弦、余弦函数的最值)(sinRxxy)(cosRxxy正弦、余弦函数的性质y=sinxyxo--1234-2-31223252722325y=sinx(xR)图象关于原点对称sin(-x)=-sinx(xR)y=sinx(xR)x6yo--12345-2-3-41是奇函数x6o--12345-2-3-41ycos(-x)=cosx(xR)y=cosx(xR)是偶函数定义域关于原点对称三、正弦、余弦函数的奇偶性正弦、余弦函数的性质四、正弦函数的单调性y=sinx(xR)增区间为[，]其值从-1增至122xyo--1234-2-31223252722325xsinx2223…0………-1010-1减区间为[，]其值从1减至-1223[+2k,+2k],kZ22[+2k,+2k],kZ223正弦、余弦函数的性质五、余弦函数的单调性正弦、余弦函数的性质y=cosx(xR)xcosx22-……0……-1010-1增区间为其值从-1增至1[+2k,2k],kZ减区间为，其值从1减至-1[2k,2k+],kZyxo--1234-2-312232527223...