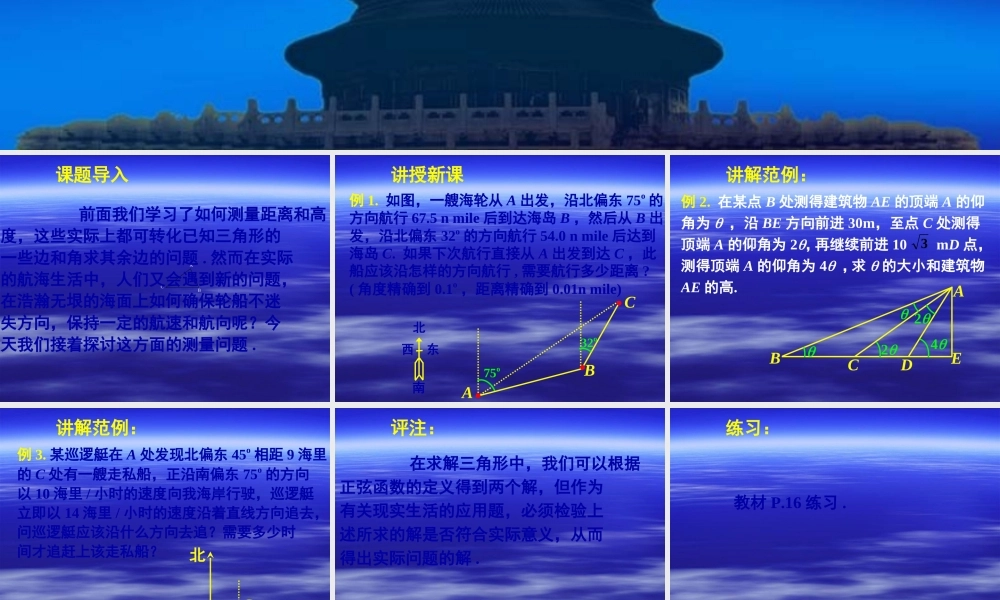
1.2应用举例(三)课题导入BCA前面我们学习了如何测量距离和高度,这些实际上都可转化已知三角形的一些边和角求其余边的问题.然而在实际的航海生活中,人们又会遇到新的问题,在浩瀚无垠的海面上如何确保轮船不迷失方向,保持一定的航速和航向呢?今天我们接着探讨这方面的测量问题.讲授新课例1.如图,一艘海轮从A出发,沿北偏东75o的方向航行67.5nmile后到达海岛B,然后从B出发,沿北偏东32o的方向航行54.0nmile后达到海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离?(角度精确到0.1o,距离精确到0.01nmile)CAB32o75o北西东南讲解范例:3AEBCD242例2.在某点B处测得建筑物AE的顶端A的仰角为,沿BE方向前进30m,至点C处测得顶端A的仰角为2,再继续前进10mD点,测得顶端A的仰角为4,求的大小和建筑物AE的高.例3.某巡逻艇在A处发现北偏东45o相距9海里的C处有一艘走私船,正沿南偏东75o的方向以10海里/小时的速度向我海岸行驶,巡逻艇立即以14海里/小时的速度沿着直线方向追去,问巡逻艇应该沿什么方向去追?需要多少时间才追赶上该走私船?北CAB讲解范例:评注:在求解三角形中,我们可以根据正弦函数的定义得到两个解,但作为有关现实生活的应用题,必须检验上述所求的解是否符合实际意义,从而得出实际问题的解.教材P.16练习.练习:课堂小结解三角形的应用题时,通常会遇到两种情况:(1)已知量与未知量全部集中在一个三角形中,依次利用正弦定理或余弦定理解之.(2)已知量与未知量涉及两个或几个三角形,这时需要选择条件足够的三角形优先研究,再逐步在其余的三角形中求出问题的解.湖南省长沙市一中卫星远程学校1.阅读必修5教材P.16到P.18;2.《习案》作业六.课后作业湖南省长沙市一中卫星远程学校