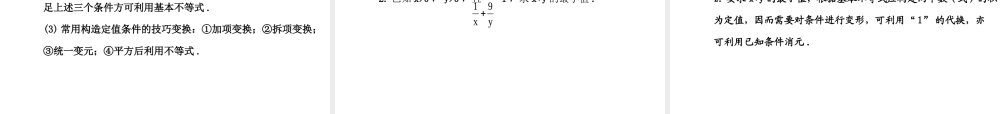第2课时基本不等式的应用1.掌握基本不等式及其变形的应用.2.会用基本不等式解决简单的最值问题及实际问题.1.基本不等式与最值设x,y为正实数.(1)若x+y=s(定值),则当________时,xy有最大值____.(2)若xy=p(定值),则当_________时,x+y有最小值_____.sxy22s4xyp2p2.利用基本不等式求积的最大值或求和的最小值时,需满足(1)x,y必须是_____.(2)求积xy的最大值时,应看和x+y是否为_____;求和x+y的最小值时,应看积xy是否为_____.正数定值定值1.已知x<-2,则函数y=的最大值为()【解析】选C.因为x<-2,所以x+2<0,故选C.12xx2A.22B.224C.224D.221y2x24x2122(x2)4224x2,2.若是2a与2b的等比中项,则ab的最大值为____.【解析】由已知条件知2a·2b=8得a+b=3,所以当且仅当a=b=时取等号.答案:2222ab39ab()()224,32943.把总长为16m的篱笆围成一个矩形场地,则矩形场地的最大面积是m2.【解析】设一边长为xm,则另一边长可表示为(8-x)m,则面积S=x(8-x)≤=16,当且仅当x=4时取等号,故当矩形的长与宽相等,都为4m时面积取到最大值16m2.答案:162x8x()2利用基本不等式求函数最值探究1:根据基本不等式“(x>0,y>0),当且仅当x=y时,等号成立”,思考下列问题:(1)若x+y=xy,如何求x+y和xy的范围?xyxy2提示:因为所以xy≤又x+y=xy,所以x+y≤整理得(x+y)2-(x+y)≥0,从而可求得x+y的范围.因为xy≤x+y=xy,所以xy≤整理得(xy)2-4xy≥0,可求得xy的范围.xyxy2,2xy()2,2xy()2,142xy()2,2xy()2,(2)常用的构造定值条件的变换方法有哪些?提示:①加项变换;②拆项变换;③统一变元;④平方后利用基本不等式.探究2:利用基本不等式解决实际问题中的最值,应注意哪些问题?提示:解实际问题要注意以下几点:①设变量时一般要把求最大或最小值的变量定义为函数;②根据实际问题抽象出函数的解析式后,只需利用基本不等式求得函数的最值;③在求函数的最值时,一定要在定义域(使实际问题有意义的自变量的取值范围)内求解.【探究总结】利用基本不等式求函数最值的三个条件(1)正:函数的解析式中,各项均为正数.(2)定:函数解析式中,含变量的各项的和或积必须有一个为定值.(3)相等:函数的解析式中,含变量的各项均相等,取得最值时必须验证等号是否成立.简记为:一正二定三相等.【拓展延伸】求条件...