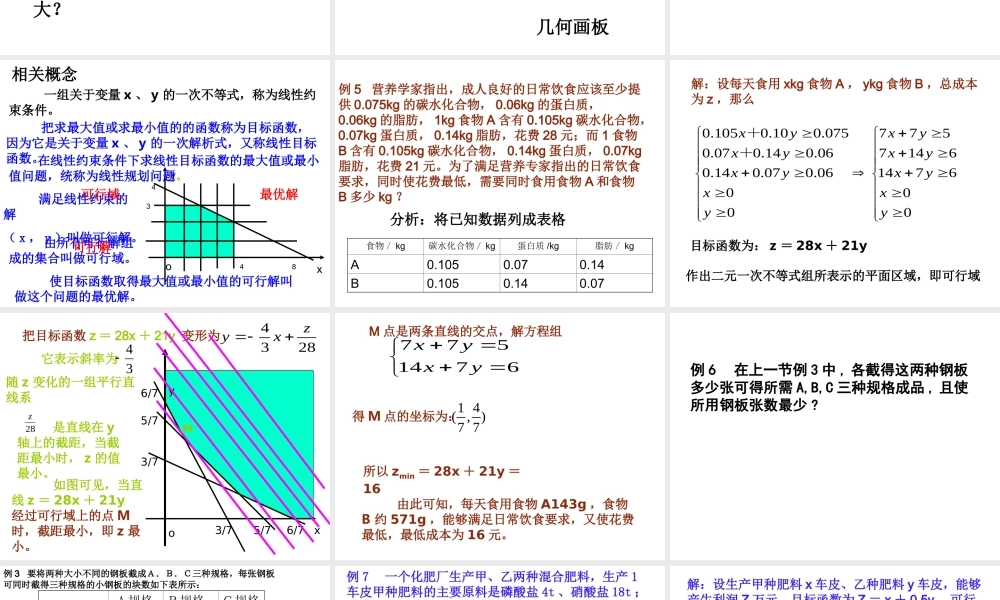
xyo3.3.2简单的线性规划问题引例•某工厂有A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,该厂所有可能的日生产安排是什么?解决问题•((11)用不等式组表示问题中的限制条件:)用不等式组表示问题中的限制条件:设甲、乙两种产品设甲、乙两种产品分别生产分别生产xx、、yy件,件,由已知条件可得二由已知条件可得二元一次不等式组:元一次不等式组:2841641200xyxyxy解决问题•((22)画出不等式组所表示的平面区域:)画出不等式组所表示的平面区域:如图,图中的阴影部分的整点(坐标为整数的点)就代表所有可能的日生产安排。Oxyx–y=6解决问题•((33)提出新问题:)提出新问题:进一步,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?解决问题•((44)尝试解答:)尝试解答:设工厂获得的利润为z,则z=2x+3y,——求z的最大值。的直线表示3,32,332zbkzxy几何画板解决问题•((55)获得结果:)获得结果:每天生产甲产品4件,乙产品2件时,工厂可获得最大利润14万元相关概念yx4843o把求最大值或求最小值的的函数称为目标函数,因为它是关于变量x、y的一次解析式,又称线性目标函数。满足线性约束的解(x,y)叫做可行解。在线性约束条件下求线性目标函数的最大值或最小值问题,统称为线性规划问题。一组关于变量x、y的一次不等式,称为线性约束条件。由所有可行解组成的集合叫做可行域。使目标函数取得最大值或最小值的可行解叫做这个问题的最优解。可行域可行解最优解例5营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?食物/kg碳水化合物/kg蛋白质/kg脂肪/kgA0.1050.070.14B0.1050.140.07分析:将已知数据列成表格解:设每天食用xkg食物A,ykg食物B,总成本为z,那么00671461475770006.007.014.006.014.007.0075.010.0105.0yxyxyxyxyxyxyxyx++目标函...