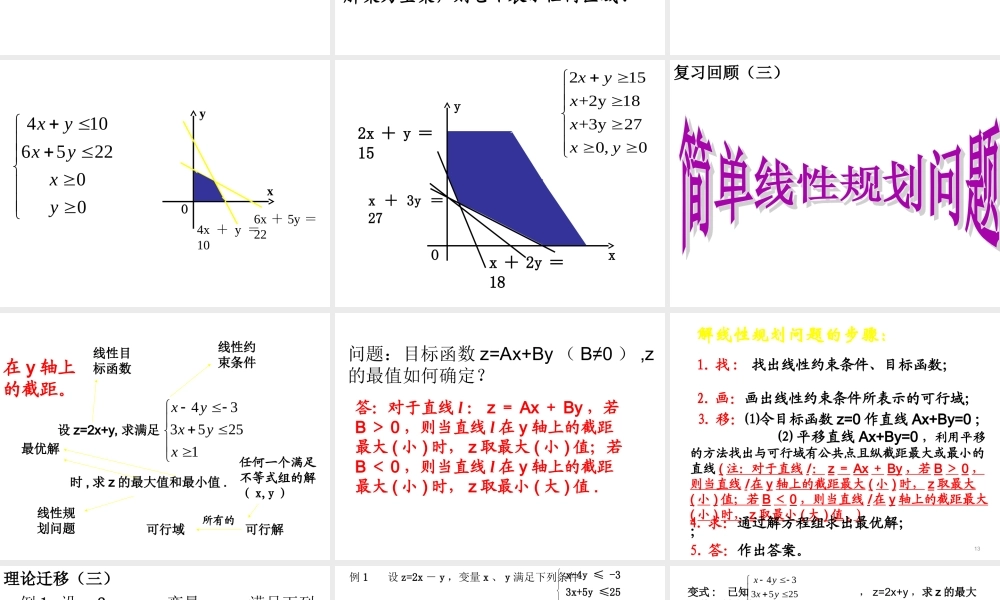
复习回顾(一)2.包括边界的区域将边界画成,不包括边界的区域将边界画成.1.画二元一次不等式表示的平面区域,常采用的方法,当边界不过原点时,常把原点作为。3.不等式Ax+By+C>0表示的平面区域位置与A、B的符号有关(同为正,异为负),相关理论不要求掌握.直线定界,特殊点定域特殊点实线虚线4x-3y≤12理论迁移(一)例1画出下列不等式表示的平面区域.(1)x+4y<4;(2)4x-3y≤12.x+4y<4xyOxyO143-4复习回顾(二)1.不等式组表示的平面区域是各个不等式所表示的平面区域的,即各个不等式所表示的平面区域的.2.不等式组表示的平面区域可能是一个多边形,也可能是一个无界区域,还可能由几个子区域合成.若不等式组的解集为空集,则它不表示任何区域.交集公共部分练习二:请画出下列不等式组表示的平面区域.410652200xyxyxy215+2y18+3y270,0xyxxxy(1)(2)理论迁移(二)xyO410652200xyxyxy6x+5y=224x+y=10215+2y18+3y270,0xyxxxy2x+y=15x+3y=27x+2y=18Oxy复习回顾(三)1255334xyxyx设z=2x+y,求满足时,求z的最大值和最小值.线性目标函数线性约束条件线性规划问题任何一个满足不等式组的解(x,y)可行解可行域所有的最优解目标函数所表示的几何意义:在y轴上的截距。问题:目标函数z=Ax+By(B≠0),z的最值如何确定?答:对于直线l:z=Ax+By,若B>0,则当直线l在y轴上的截距最大(小)时,z取最大(小)值;若B<0,则当直线l在y轴上的截距最大(小)时,z取最小(大)值.13解线性规划问题的步骤:2.画:画出线性约束条件所表示的可行域;3.移:⑴令目标函数z=0作直线Ax+By=0;⑵平移直线Ax+By=0,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线(注:对于直线l:z=Ax+By,若B>0,则当直线l在y轴上的截距最大(小)时,z取最大(小)值;若B<0,则当直线l在y轴上的截距最大(小)时,z取最小(大)值.);4.求:通过解方程组求出最优解;5.答:作出答案。1.找:找出线性约束条件、目标函数;,求z的最大值和最小值.yX0123456712345x-4y+3=03x+5y-25=0x=1例1.设z=2x-y,变量x、y满足下列条件x-4y≤-33x+5y≤25x≥1理论迁移(三)解:不等式组表示的平面区域如图所示:5yX012346712345x-4y+3=03x+5y-25=0x=12x-y=0BBAACC代入点B得最大为8,代入点A得最小值为.125-,求z的最大值和最小值.3x+...