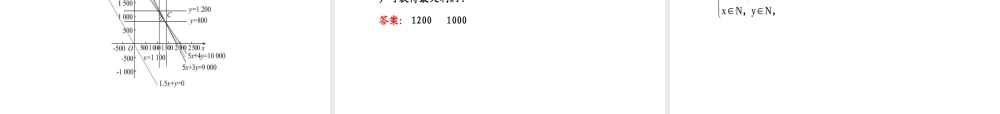第2课时简单线性规划的应用类型一线性规划的实际应用问题1.(2013·湖北高考)某旅行社租用A,B两种型号的客车安排900名客人旅行,A,B两种车辆的载客量分别为36人和60人,租金分别为1600元/辆和2400元/辆,旅行社要求租车总数不超过21辆,且B型车不多于A型车7辆.则租金最少为()A.31200元B.36000元C.36800元D.38400元2.某家具厂有木料90m3,五合板600m2,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1m3,五合板2m2,生产每个书橱需要方木料0.2m3,五合板1m2,出售一张书桌可获利润80元,出售一个书橱可获利润120元.(1)如果只安排生产书桌,可获利润多少.(2)如果只安排生产书橱,可获利润多少.(3)怎样安排生产可使所获利润最大.【解题指南】1.把实际问题转化为线性规划问题求解.2.设生产书桌x张,生产书橱y个,可得目标函数为z=80x+120y.(1)求当y=0时的最大利润,(2)求当x=0时的最大利润,(3)找出约束条件,画出可行域,利用线性规划解题.【自主解答】1.选C.设A型、B型车辆的数量分别为x,y辆,则相应的租金为1600x+2400y,依题意,x,y还需满足:x+y≤21,y≤x+7,36x+60y≥900,于是问题等价于求满足约束条件且使目标函数z=1600x+2400y达到最小xy21yx736x60y900xy0xyN,,,,,,,的x,y,作可行域如图所示,可行域的三个顶点坐标分别为P(5,12),Q(7,14),R(15,6),由图可知,当直线z=1600x+2400y经过可行域的点P时,直线z=1600x+2400y在y轴上的截距最小,即z取得最小值.故应配备A型车5辆,B型车12辆.zmin=1600x+2400y=1600×5+2400×12=36800(元).z24002.设生产书桌x张,生产书橱y个,利润为z元,则目标函数为z=80x+120y,根据题知,约束条件为画出可行域如图所示,0.1x0.2y90x2y9002xy6002xy600x0y0x0y0xNyNxNyN,,,,即,,,,,,,,(1)若只生产书桌,则y=0,此时目标函数z=80x,由图可知zmax=80×300=24000,即只生产书桌,可获利润24000元.(2)若只生产书橱,则x=0,此时目标函数z=120y,由图可知zmax=120×450=54000,即只生产书橱,可获利润54000元.(3)作直线l:80x+120y=0,并平移直线l,由图可知,当直线l过点C时,z取得最大值,解得C(100,400),所以zmax=80×100+120×400=56000,即生产100张书桌,400个书橱,可获得最大利润.x2y9002xy600,,【规律总结】解决线性规划的实际问题的步骤(1)转化:设出未...