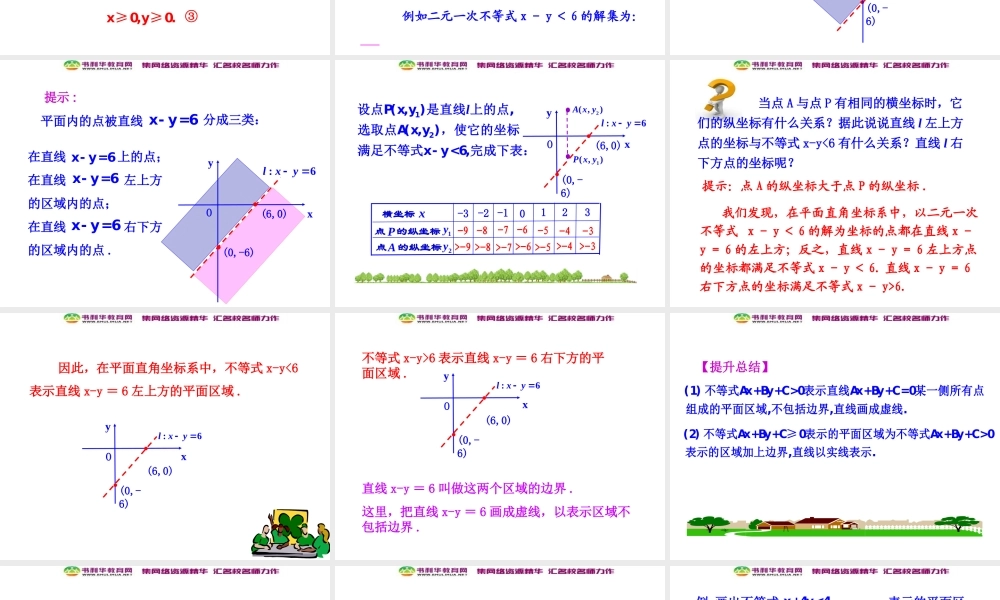
3.3二元一次不等式(组)与简单的线性规划问题3.3.1二元一次不等式(组)与平面区域第1课时二元一次不等式表示的平面区域一家银行的信贷部计划年初投入25000000元用于企业和个人贷款,希望这笔资金至少可带来30000元的收益,其中企业贷款获益12%,个人贷款获益10%.上述问题应该用什么不等式模型来刻画呢?1.了解二元一次不等式的实际背景.2.了解二元一次不等式的几何意义.3.能正确地使用平面区域表示二元一次不等式.(难点)设用于企业贷款的资金为x元,用于个人贷款的资金为y元.由资金总数为25000000元,得到1.二元一次不等式:含有两个未知数,并且未知数的次数是1的不等式.x+y≤25000000.①探究点1二元一次不等式的有关概念由于预计企业贷款创收12%,个人贷款创收10%,共创收30000元以上,所以0000(12)x+(10)y≥30000,12x+10y≥3000000.即②最后考虑到用于企业贷款和个人贷款的资金数额都不能是负值,所以x≥0,y≥0.③2.二元一次不等式的解集:满足二元一次不等式的x和y的取值构成有序数对(x,y),所有这样的有序数对(x,y)构成的集合称为二元一次不等式的解集.有序数对可以看成直角坐标平面内点的坐标.于是,二元一次不等式的解集就可以看成直角坐标系内的点构成的集合.例如二元一次不等式x-y<6的解集为::6lxy(0,-6)(6,0)xOy以二元一次不等式的解为坐标的点的集合表示什么平面图形?x-y<6(x,y)x-y<6探究点2二元一次不等式与平面区域在直线上的点;在直线左上方的区域内的点;在直线右下方的区域内的点.平面内的点被直线x-y=6x-y=6xO:6lxy(0,-6)(6,0)y分成三类:x-y=6x-y=6提示:xO:6lxy(0,-6)(6,0)y12设点P(x,y)是直线上的点,选取点A(x,y),使它的坐标满足不等式x-y<6,完成下表:l1(,)Pxy2(,)Axy横坐标x点的纵坐标P1y点的纵坐标A2y-3-2-10123-9-8-7-6-5-4-3>-9>-8>-7>-6>-5>-4>-3当点A与点P有相同的横坐标时,它们的纵坐标有什么关系?据此说说直线l左上方点的坐标与不等式x-y<6有什么关系?直线l右下方点的坐标呢?我们发现,在平面直角坐标系中,以二元一次不等式x-y<6的解为坐标的点都在直线x-y=6的左上方;反之,直线x-y=6左上方点的坐标都满足不等式x-y<6.直线x-y=6右下方点的坐标满足不等式x-y>6.提示:点A的纵坐标大于点P的纵坐标.因此,在平面直角坐标系中,不等式x-y<6表示直线x-y=6左上方的平面区域.xO:6lxy(0,-6)(6,0)yxO:6lxy(0,-6)(6,0)y不等式x-y>6表示直线x-y=6右下方的平面区域.直线x-...