人教版高中数学必修五同课异构课件：2.4 第2课时 等比数列的性质 情境互动课型 .pptVIP免费

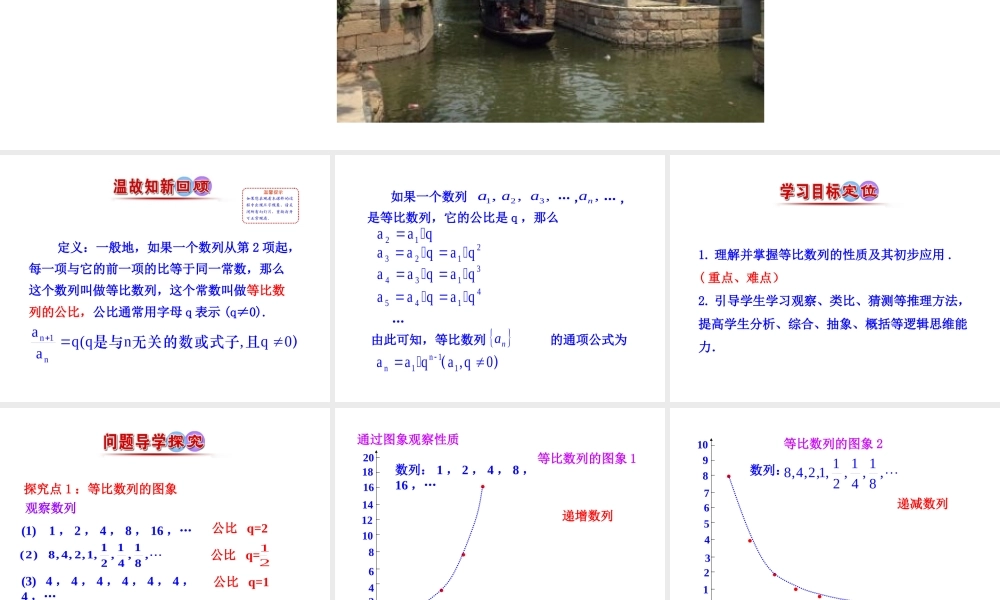
第2课时等比数列的性质定义：一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同一常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母q表示(q≠0).n1naq(qn,q0a是与无关的数或式子且）如果一个数列是等比数列，它的公比是q，那么,1a,2a,3a,na…，…，21aaq由此可知，等比数列的通项公式为na2321aaqaq3431aaqaq4541aaqaqn1n11aaqa,q0（）…1.理解并掌握等比数列的性质及其初步应用.(重点、难点）2.引导学生学习观察、类比、猜测等推理方法，提高学生分析、综合、抽象、概括等逻辑思维能力．(1)1，2，4，8，16，…观察数列111(2)8,4,2,1,,,,248(3)4，4，4，4，4，4，4，…(4)1，-1，1，-1，1，-1，1，…公比q=2公比q=12公比q=1公比q=-1探究点1：等比数列的图象等比数列的图象1数列：1，2，4，8，16，…123456789102468101214161820O●●●●●递增数列通过图象观察性质等比数列的图象212345678910O数列：●●●●,81,41,21,1,2,4,8●●●12345678910递减数列等比数列的图象3123456789102468101214161820O数列：4，4，4，4，4，4，4，…●●●●●●●●●●常数列等比数列的图象412345678910O12345678910●●●●●●●●●●数列：1，-1，1，-1，1，-1，1，摆动数列-1在6和768之间插入6个数，使它们组成共8项的等比数列，则这个等比数列的第6项是________．【解析】a8＝a1q7,768＝6q7，∴q＝2，∴a6＝6×25＝192.【即时练习】192类比等差数列的性质，等比数列有哪些性质呢？探究点2：等差、等比数列的性质比较an-an-1=d（n≥2）等差数列等比数列常数减—除加—乘dnaan)1(1)0(111qaqaann加-乘乘—乘方迭加法迭乘法等比数列用“比”代替了等差数列中的“差”定义数学表达式通项公式证明通项公式1(0n2)nnaqqa，,提示:由等差数列的性质，猜想等比数列的性质{an}是公差为d的等差数列{bn}是公比为q的等比数列性质1：an=am+(n-m)d性质2：若an-k,an,an+k是{an}中的三项，则2an=an+k+an-k猜想2：性质3：若n+m=p+q,则am+an=ap+aq猜想1：nmnmbbq若bn-k,bn,bn+k是{bn}中的三项,则若n+m=p+q，则bn·bm=bp·bq2nnknkbbb猜想3：性质4：从原数列中取出偶数项组成的新数列公差为2d.(可推广)性质5:若{cn}是公差为d′的等差数列，则数列{an+cn}是公差为d+d′的等差数列.若{dn}是公比为q′的等比数列,则数列{bn•dn}是公比为q·q′...