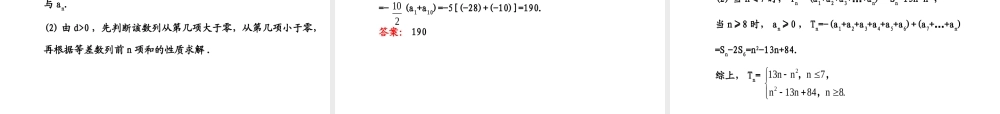一、等差数列前n项和的最值问题等差数列前n项和公式为当d≠0时,Sn是关于n的二次函数,在一定条件下,Sn有最值.请根据这些条件思考下面的问题:第2课时等差数列习题课探究1:在等差数列{an}中,当a1>0,d<0时,Sn有最大值还是有最小值?a1<0,d>0呢?提示:当a1>0,d<0时,数列为递减数列,所以Sn有最大值;当a1<0,d>0时,数列为递增数列,所以Sn有最小值.探究2:从函数观点分析Sn=的最值情况.提示:当d>0时,此二次函数的开口向上,Sn存在最小值;当d<0时,此二次函数的开口向下,Sn存在最大值.21ddn(a)n22【探究总结】对等差数列前n项和最值的三点说明(1)等差数列前n项和的最值不一定在顶点处取得.(2)取最值时的n值,一定是正整数.(3)d=0时,数列为常数列,前n项和Sn=na1,是关于n的一次函数.二、数列{|an|}的前n项和问题等差数列{an}的首项为a1,公差为d,则其前n项和为Sn=na1+.将数列{an}的每一项都取绝对值,得到一新数列{|an|},请思考下面的问题:nn1d2探究1:若等差数列{an}的首项a1<0,公差为d>0,其前n项和为Sn,则数列{|an|}的前n项和如何求?提示:因为等差数列{an}的首项a1<0,公差为d>0,所以存在正整数m,当n>m时,有an>0,当n≤m时,有an≤0,记数列{|an|}的前n项和为Tn,则当n≤m时,Tn=|a1|+|a2|+…+|an|=-Sn,当n>m时Tn=|a1|+|a2|+…+|am|+am+1+…+an=-a1-a2-…-am+am+1+…+an=a1+a2+…+am+am+1+…+an-2(a1+a2+…+am)=Sn-2Sm.所以Tn=nnmSnmS2Snm.,,,>探究2:若等差数列{an}的首项a1>0,公差d<0,其前n项和为Sn,则数列{|an|}的前n项和如何求?提示:因为等差数列{an}的首项a1>0,公差d<0,所以存在正整数m,当n>m时,有an≤0,当n≤m时有an>0,记数列{|an|}的前n项和为Tn,则当n≤m时,Tn=a1+a2+…+an=Sn,当n>m时,Tn=a1+a2+…+am+|am+1|+…+|an|=a1+a2+…+am-am+1-…-an=-a1-a2-…-am-am+1-…-an+2(a1+a2+…+am)=-Sn+2Sm.所以Tn=nnmSnmS2Snm.,,,>【探究总结】求等差数列{|an|}的前n项和两点说明(1)当数列中含有负项时,要注意对n的讨论.(2)数列{|an|}的前n项和要以分段的形式表示.类型一求等差数列前n项和的最值1.在递减等差数列{an}中,若a1+a100=0,则其前n项和Sn取最大值时的n值为()A.49B.51C.48D.502.(2014·江西高考)在等差数列{an}中,a1=7,公差为d,前n项和为Sn,当且仅当n=8时Sn取得最大值,则d的取值范围为.3.已知数列{an}的前n项和公式为Sn=2n2-30n.(1)求数列{an}的通...