人教A版数学选修2-3全册课件：第二章 2.3 2.3.2 离散型随机变量的方差.pptVIP免费

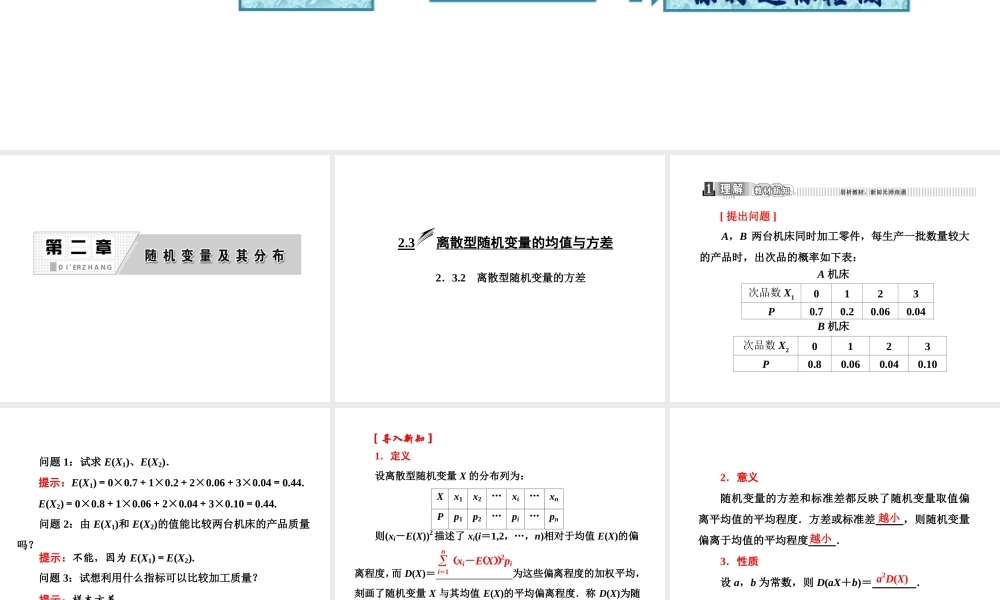
第二章2.32.3.2离散型随机变量的方差2突破常考题型题型一1理解教材新知题型二3跨越高分障碍4应用落实体验随堂即时演练课时达标检测题型三2.3离散型随机变量的均值与方差2．3.2离散型随机变量的方差[提出问题]A，B两台机床同时加工零件，每生产一批数量较大的产品时，出次品的概率如下表：A机床次品数X10123P0.70.20.060.04B机床次品数X20123P0.80.060.040.10问题1：试求E(X1)、E(X2)．提示：E(X1)＝0×0.7＋1×0.2＋2×0.06＋3×0.04＝0.44.E(X2)＝0×0.8＋1×0.06＋2×0.04＋3×0.10＝0.44.问题2：由E(X1)和E(X2)的值能比较两台机床的产品质量吗？提示：不能，因为E(X1)＝E(X2)．问题3：试想利用什么指标可以比较加工质量？提示：样本方差．[导入新知]1．定义设离散型随机变量X的分布列为：Xx1x2…xi…xnPp1p2…pi…pn则(xi－E(X))2描述了xi(i＝1,2，…，n)相对于均值E(X)的偏离程度，而D(X)＝为这些偏离程度的加权平均，刻画了随机变量X与其均值E(X)的平均偏离程度．称D(X)为随机变量X的方差，其为随机变量X的标准差．i＝1nxi－EX2pi算术平方根DX2．意义随机变量的方差和标准差都反映了随机变量取值偏离平均值的平均程度．方差或标准差，则随机变量偏离于均值的平均程度．3．性质设a，b为常数，则D(aX＋b)＝．越小越小a2D(X)4．两点分布和二项分布的方差XX服从两点分布X～B(n，p)D(X)(其中p为成功概率)p(1－p)np(1－p)[化解疑难]随机变量的方差与样本方差的关系随机变量的方差即为总体的方差，它是一个常数，不随抽样样本而客观存在的；样本方差则是随机变量，它是随样本不同而变化的．求离散型随机变量的方差[例1]袋中有大小相同的小球6个，其中红球2个、黄球4个，规定取1个红球得2分，1个黄球得1分．从袋中任取3个小球，记所取3个小球的分数之和为X，求随机变量X的分布列、均值和方差．[解]由题意可知，X的所有可能的取值为5,4,3.P(X＝5)＝C22C14C36＝15；P(X＝4)＝C12C24C36＝35；P(X＝3)＝C34C36＝15.故X的分布列为X543P153515E(X)＝5×15＋4×35＋3×15＝4.D(X)＝(5－4)2×15＋(4－4)2×35＋(3－4)2×15＝25.[类题通法]1．离散型随机变量的分布列、均值和方差是三个紧密联系的有机统一体，一般在试题中综合在一起考查，其关键是求出分布列．2．在求分布列时，要注意利用等可能事件、互斥事件，相互独立事件的概率公式计算概率，并注意结合分布列的性质，简化概率计算．[活学活用]编号为1,2,3的三位同学随意入座编号为1,2,3的...