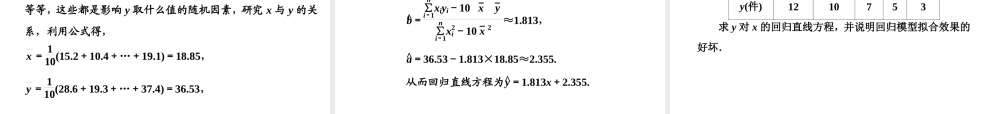人教A版数学选修2-3全册课件：第三章 3.1 回归分析的基本思想及其初步应用.pptVIP免费

第三章3.1回归分析的基本思想及其初步应用2突破常考题型题型一1理解教材新知题型二题型三3跨越高分障碍4应用落实体验随堂即时演练课时达标检测知识点一知识点二3.1回归分析的基本思想及其初步应用[提出问题]《必修3》中，求出回归直线方程y^＝b^x＋a^.问题1：回归直线方程准确的反映了x，y之间的关系吗？回归直线方程提示：不是．问题2：所有的两个相关变量都可以求回归方程吗？提示：可以，但拟合程度很差．[导入新知]1．回归分析回归分析是对具有的两个变量进行统计分析的一种常用方法．2．回归直线方程方程y^＝b^x＋a^是两个具有线性相关关系的变量的一组数据(x1，y1)(x2，y2)，…，(xn，yn)的回归方程，其中a^，b^是待定参数，其最小二乘估计分别为：相关关系b^＝i＝1nxi－xyi－yi＝1nxi－x2＝i＝1nxiyi－nxyi＝1nx2i－nx2，a^＝y－b^x，其中x＝1ni＝1nxi，y＝1ni＝1nyi，称为样本点的中心．(x，y)[化解疑难]线性回归方程中系数b^的含义(1)b^是回归直线的斜率的估计值，表示x每增加一个单位，y的平均增加单位数，而不是增加单位数．(2)当b^＞0时，变量y与x具有正的线性相关关系；当b^＜0时，变量y与x具有负的线性相关关系．线性回归分析[提出问题]具有相关关系的两个变量的回归直线方程y^＝b^x＋a^.问题1：预报变量y^与真实值y一样吗？提示：不一定．问题2：预报值y^与真实值y之间误差大了好还是小了好？提示：越小越好．[导入新知]1．残差平方和法(1)e^i＝yi－y^i＝yi－b^xi－a^(i＝1,2，…，n)，称为相应于点(xi，yi)的残差．(2)残差平方和越小，模型拟合效果越好．2．残差图法残差点落在水平的带状区域内，说明选用的模型比较合适，其中这样的带状区域宽度，说明模型的精确度越高．i＝1n(yi－y^i)2比较均匀地越窄3．利用相关指数R2刻画回归效果其计算公式为：R2＝，其几何意义：，表示回归效果越好．1－i＝1nyi－y^i2i＝1nyi－y2R2越接近于1[化解疑难]1．在线性回归模型中，因为e是一个随机变量，所以可以通过其数字特征来刻画它的一些总体特征．2．在线性回归模型中，R2表示解释变量对于预报变量变化的贡献率，R2越接近于1，表示回归的效果越好．求线性回归方程[例1]某种产品的广告费用支出x与销售额y(单位：百万元)之间有如下的对应数据：x/百万元24568y/百万元3040605070(1)画出散点图；(2)求线性回归方程；(3)试预测广告费用支出为10百万元时，销售额多大？[解](1)散点图...