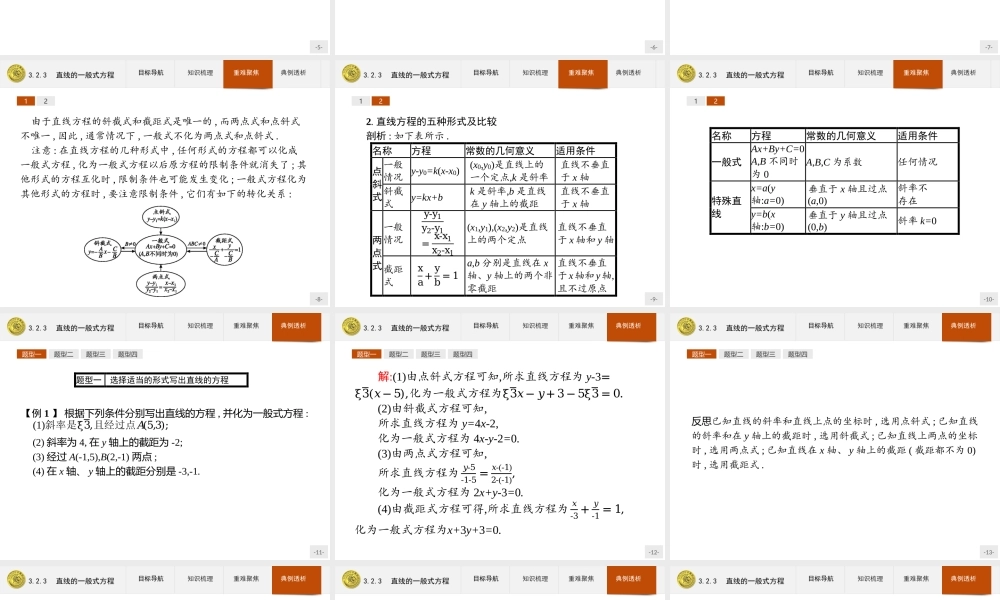
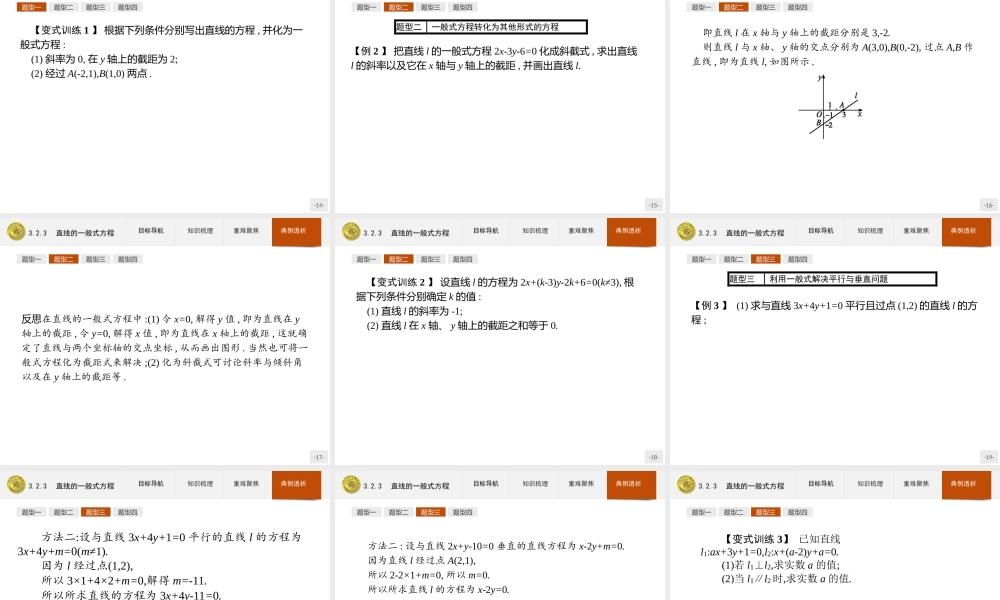
-1-3.2.3直线的一般式方程-2-3.2.3直线的一般式方程目标导航知识梳理重难聚焦典例透析1.掌握直线的一般式方程,明确各系数的意义.2.掌握一般式与其他形式的互化.3.了解二元一次方程与直线的对应关系.-3-3.2.3直线的一般式方程目标导航知识梳理重难聚焦典例透析直线的一般式方程(1)定义:关于x,y的二元一次方程Ax+By+C=0(其中A,B不同时为0)叫做直线的一般式方程,简称一般式.(2)适用范围:在平面直角坐标系中,任何一条直线都可用一般式表示.(3)系数的几何意义:①当B≠0时,则−𝐴𝐵=𝑘(斜率),−𝐶𝐵=𝑏(𝑦轴上的截距);②当B=0,A≠0时,则−𝐶𝐴=𝑎(𝑥轴上的截距),此时斜率不存在.-4-3.2.3直线的一般式方程目标导航知识梳理重难聚焦典例透析知识拓展1.当AB>0时,k<0,倾斜角α为钝角;当AB<0时,k>0,倾斜角α为锐角;当A=0,B≠0时,k=0,倾斜角α=0°;当B=0,A≠0时,k不存在,倾斜角α=90°.2.二元一次方程与直线的关系:二元一次方程的每一组解都可以看成是平面直角坐标系中一个点的坐标,这个方程的全体解组成的集合,就是坐标满足二元一次方程的全体点的集合,这些点的集合就组成了一条直线.二元一次方程与平面直角坐标系中的直线是一一对应的.-5-3.2.3直线的一般式方程目标导航知识梳理重难聚焦典例透析【做一做1】若方程Ax+By+C=0表示直线,则A,B应满足的条件为()A.A≠0B.B≠0C.A·B≠0D.A2+B2≠0解析:A,B不能同时为0,则A2+B2≠0.答案:D-6-3.2.3直线的一般式方程目标导航知识梳理重难聚焦典例透析【做一做2】直线2x+y+4=0的斜率k=.答案:-2-7-3.2.3直线的一般式方程目标导航知识梳理重难聚焦典例透析121.直线方程的一般式与其他形式的互化剖析:一般式化斜截式的步骤:(1)移项,By=-Ax-C;(2)当B≠0时,得斜截式y=−𝐴𝐵𝑥−𝐶𝐵.一般式化截距式的步骤:(1)把常数项移到方程右边,得Ax+By=-C;(2)当C≠0时,方程两边同除以-C,得𝐴𝑥-𝐶+𝐵𝑦-𝐶=1;(3)化为截距式𝑥-𝐶𝐴+𝑦-𝐶𝐵=1.-8-3.2.3直线的一般式方程目标导航知识梳理重难聚焦典例透析12由于直线方程的斜截式和截距式是唯一的,而两点式和点斜式不唯一,因此,通常情况下,一般式不化为两点式和点斜式.注意:在直线方程的几种形式中,任何形式的方程都可以化成一般式方程,化为一般式方程以后原方程的限制条件就消失了;其他形式的方程互化时,限制条件也可能发生变化;一般式方程化为其他形式的方程时,要注意限制条件,它们有如下的转化关系:-9-3.2.3直线的一般式方程目标导航知识梳理重难聚焦典例透析122.直线方程的五种形式及比较...