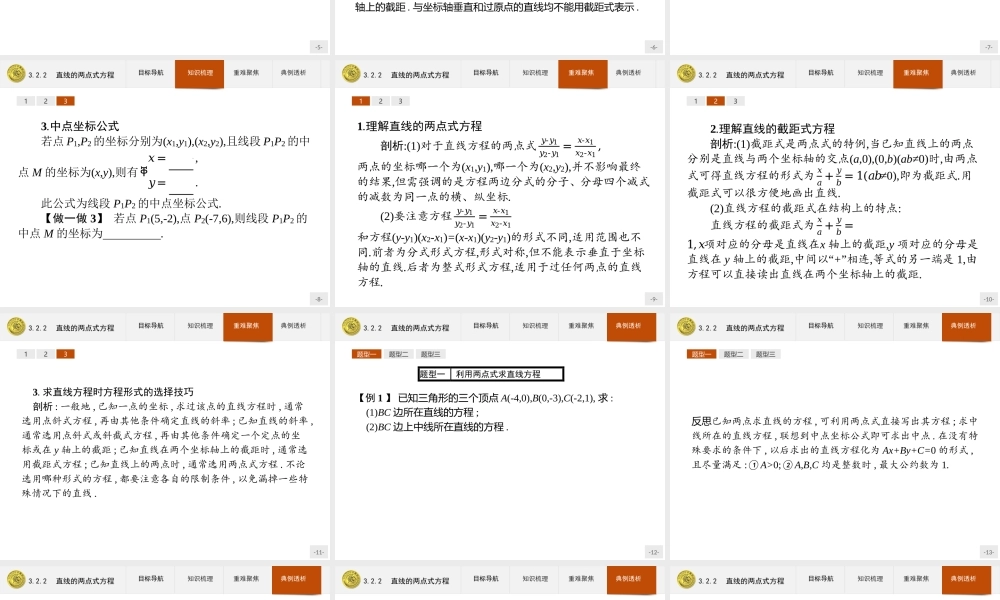
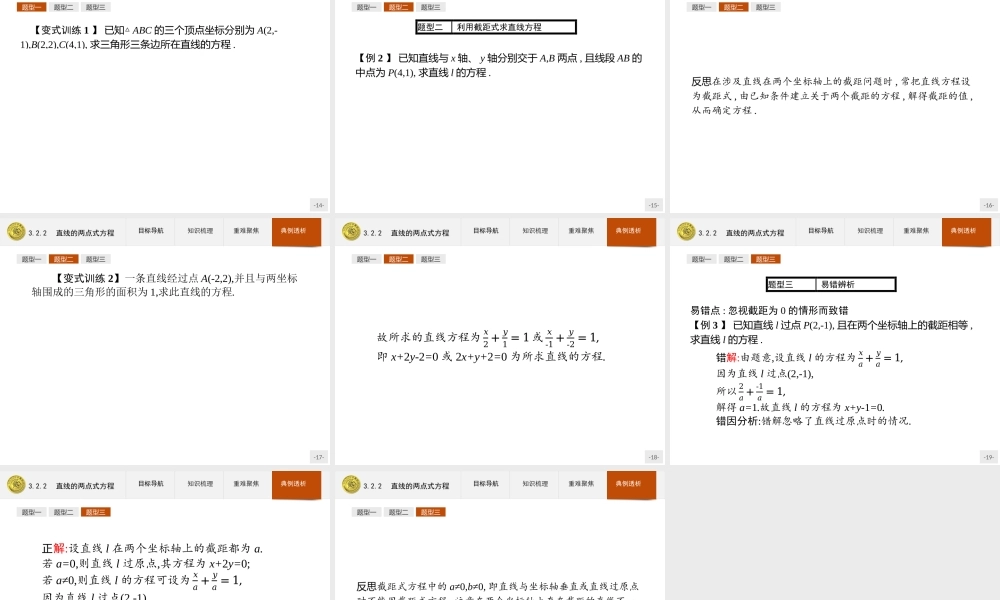
-1-3.2.2直线的两点式方程-2-3.2.2直线的两点式方程目标导航知识梳理重难聚焦典例透析1.掌握直线的两点式方程和截距式方程以及各自的适用条件.2.会选择适当的方程形式求直线方程.3.能将直线的两点式方程化为截距式和斜截式.-3-3.2.2直线的两点式方程目标导航知识梳理重难聚焦典例透析1231.直线的两点式方程(1)定义:如图,直线l经过点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2),则方程𝑦-𝑦1𝑦2-𝑦1=𝑥-𝑥1𝑥2-𝑥1叫做直线𝑙的两点式方程,简称两点式.(2)说明:与坐标轴垂直的直线不能用两点式方程表示.-4-3.2.2直线的两点式方程目标导航知识梳理重难聚焦典例透析123归纳总结直线的两点式方程应用的前提条件是:x1≠x2,y1≠y2,即直线的斜率不存在或斜率为零时,都不能用两点式方程.当x1=x2时,直线方程为x=x1;当y1=y2时,直线方程为y=y1.-5-3.2.2直线的两点式方程目标导航知识梳理重难聚焦典例透析123【做一做1】经过点A(5,6)和点B(-1,2)的直线的两点式方程是()A.𝑦-5𝑥-6=𝑦+1𝑥-2B.𝑦-62-6=𝑥-5-1-5C.2-6𝑦-6=-1-5𝑥-5D.𝑥-62-6=𝑦-5-1-5答案:B-6-3.2.2直线的两点式方程目标导航知识梳理重难聚焦典例透析1232.直线的截距式方程(1)定义:如图,直线l与两个坐标轴的交点分别是P1(a,0),P2(0,b)(其中a≠0,b≠0),则方程𝑥𝑎+𝑦𝑏=1叫做直线𝑙的截距式方程.(2)说明:一条直线与x轴的交点(a,0)的横坐标a叫做直线在x轴上的截距.与坐标轴垂直和过原点的直线均不能用截距式表示.-7-3.2.2直线的两点式方程目标导航知识梳理重难聚焦典例透析123【做一做2】在x轴、y轴上的截距分别为-3,4的直线方程是()A.𝑥-3+𝑦4=1B.𝑥3+𝑦-4=1C.𝑥-3−𝑦4=1D.𝑥4+𝑦-3=1答案:A-8-3.2.2直线的两点式方程目标导航知识梳理重难聚焦典例透析1233.中点坐标公式若点P1,P2的坐标分别为(x1,y1),(x2,y2),且线段P1P2的中点M的坐标为(x,y),则有ቐ𝑥=𝑥1+𝑥22,𝑦=𝑦1+𝑦22.此公式为线段P1P2的中点坐标公式.【做一做3】若点P1(5,-2),点P2(-7,6),则线段P1P2的中点M的坐标为.解析:𝑀ቀ5-72,-2+62ቁ,即M(-1,2).答案:(-1,2)-9-3.2.2直线的两点式方程目标导航知识梳理重难聚焦典例透析1231.理解直线的两点式方程剖析:(1)对于直线方程的两点式𝑦-𝑦1𝑦2-𝑦1=𝑥-𝑥1𝑥2-𝑥1,两点的坐标哪一个为(x1,y1),哪一个为(x2,y2),并不影响最终的结果,但需强调的是方程两边分式的分子、分母四个减式的减数为同一点的横、纵坐标.(2)要注意方程𝑦-𝑦1𝑦2-𝑦1=𝑥-𝑥1𝑥2-𝑥1和方程(y-y1)(x2-x1)=(x-x1)(y2-y1)的形式不同,适用...