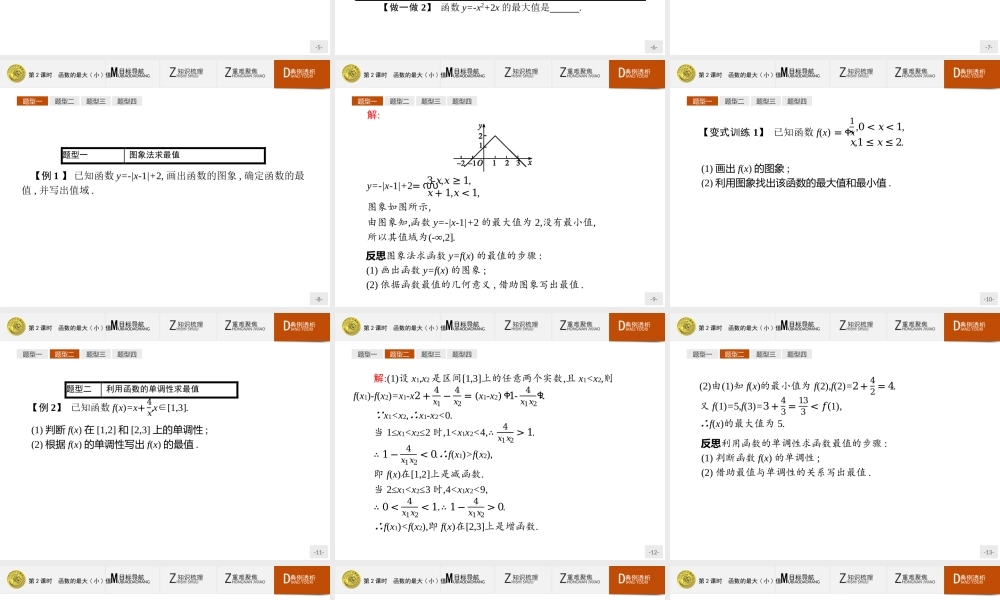
-1-第2课时函数的最大(小)值-2-第2课时函数的最大(小)值ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航1.理解函数最大值和最小值的概念,明确定义中“任意”和“存在”表达的含义.2.能借助函数的图象和单调性,求一些简单函数的最值.3.能利用函数的最值解决有关的实际应用问题.-3-第2课时函数的最大(小)值ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航121.最大值和最小值最大值最小值条件一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:对于任意的x∈I,都有f(x)≤Mf(x)≥M存在x0∈I,使得f(x0)=M结论称M是函数y=f(x)的最大值称M是函数y=f(x)的最小值几何意义f(x)图象上最高点的纵坐标f(x)图象上最低点的纵坐标-4-第2课时函数的最大(小)值ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航12知识拓展1.定义中M首先是一个函数值,它是值域的一个元素,如函数f(x)=-x2(x∈R)的最大值为0,有f(0)=0.2.最大(小)值定义中的“任意”是说对定义域内的每一个值都必须满足不等式,即对于定义域内的全部元素,都有f(x)≤M(f(x)≥M)成立,也就是说,y=f(x)的图象不能位于直线y=M的上(下)方.3.最大(小)值定义中的“存在”是说定义域中至少有一个实数满足等式,也就是说y=f(x)的图象与直线y=M至少有一个交点.-5-第2课时函数的最大(小)值ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航12【做一做1】设函数f(x)=2x-1(0≤x<1),则f(x)()A.有最大值,无最小值B.有最小值,无最大值C.既有最大值,又有最小值D.既无最大值,也无最小值解析: 函数f(x)=2x-1在x∈[0,1)上单调递增,∴f(x)在x=0时取得最小值,无最大值.答案:B-6-第2课时函数的最大(小)值ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航122.最值定义函数的最大值和最小值统称为函数的最值几何意义函数y=f(x)的最值是图象最高点或最低点的纵坐标说明函数的最值是在整个定义域内的性质归纳总结二次函数f(x)=ax2+bx+c(a≠0)在定义域R上,当a>0时,最小值是𝑓ቀ-𝑏2𝑎ቁ,不存在最大值;当a<0时,最大值是𝑓ቀ-𝑏2𝑎ቁ,不存在最小值.【做一做2】函数y=-x2+2x的最大值是.答案:1-7-第2课时函数的最大(小)值ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航函数的最值与单调性的关系剖析:(1)函数的单调...