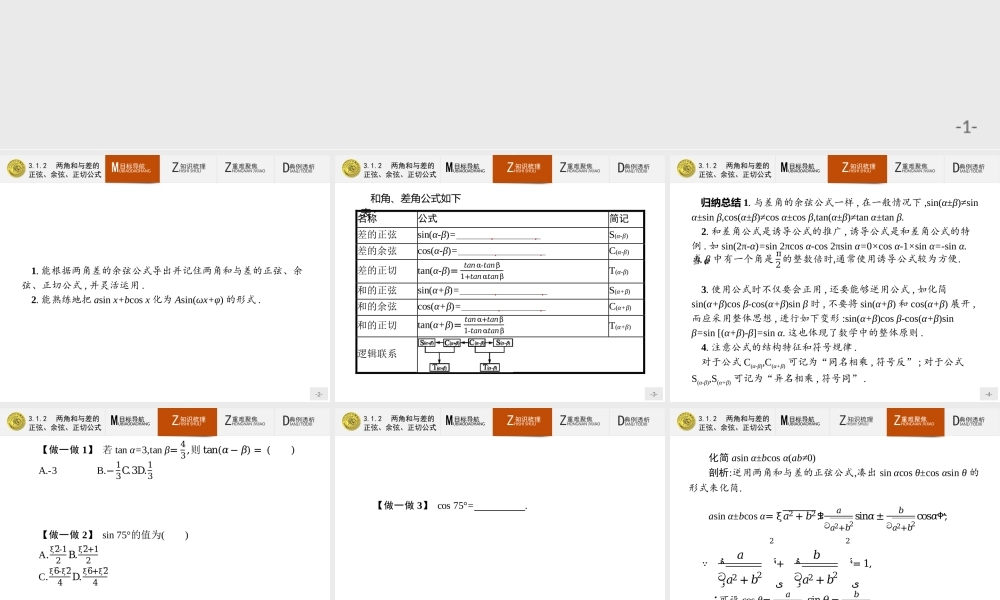
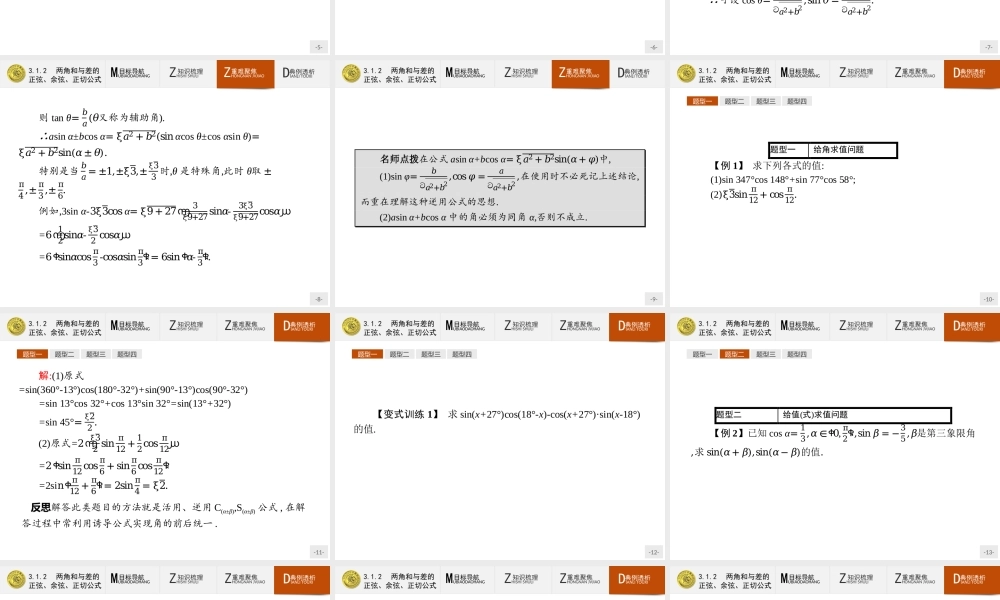
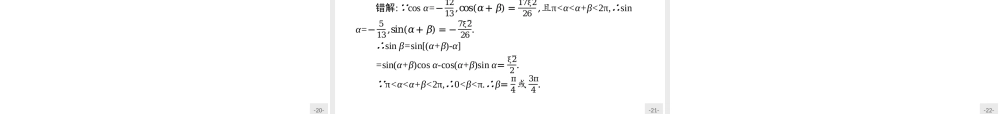-1-3.1.2两角和与差的正弦、余弦、正切公式-2-3.1.2两角和与差的正弦、余弦、正切公式ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航1.能根据两角差的余弦公式导出并记住两角和与差的正弦、余弦、正切公式,并灵活运用.2.能熟练地把asinx+bcosx化为Asin(ωx+φ)的形式.-3-3.1.2两角和与差的正弦、余弦、正切公式ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航和角、差角公式如下表:名称公式简记差的正弦sin(α-β)=sinαcosβ-cosαsinβS(α-β)差的余弦cos(α-β)=cosαcosβ+sinαsinβC(α-β)差的正切tan(α-β)=𝑡𝑎𝑛α-𝑡𝑎𝑛β1+𝑡𝑎𝑛α𝑡𝑎𝑛βT(α-β)和的正弦sin(α+β)=sinαcosβ+cosαsinβS(α+β)和的余弦cos(α+β)=cosαcosβ-sinαsinβC(α+β)和的正切tan(α+β)=𝑡𝑎𝑛α+𝑡𝑎𝑛β1-𝑡𝑎𝑛α𝑡𝑎𝑛βT(α+β)逻辑联系-4-3.1.2两角和与差的正弦、余弦、正切公式ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航或β中有一个角是π2的整数倍时,通常使用诱导公式较为方便.归纳总结1.与差角的余弦公式一样,在一般情况下,sin(α±β)≠sinα±sinβ,cos(α±β)≠cosα±cosβ,tan(α±β)≠tanα±tanβ.2.和差角公式是诱导公式的推广,诱导公式是和差角公式的特例.如sin(2π-α)=sin2πcosα-cos2πsinα=0×cosα-1×sinα=-sinα.当α3.使用公式时不仅要会正用,还要能够逆用公式,如化简sin(α+β)cosβ-cos(α+β)sinβ时,不要将sin(α+β)和cos(α+β)展开,而应采用整体思想,进行如下变形:sin(α+β)cosβ-cos(α+β)sinβ=sin[(α+β)-β]=sinα.这也体现了数学中的整体原则.4.注意公式的结构特征和符号规律.对于公式C(α-β),C(α+β)可记为“同名相乘,符号反”;对于公式S(α-β),S(α+β)可记为“异名相乘,符号同”.-5-3.1.2两角和与差的正弦、余弦、正切公式ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航【做一做1】若tanα=3,tanβ=43,则tan(𝛼−𝛽)=()A.-3B.−13C.3D.13解析:tan(α-β)=tan𝛼-tan𝛽1+tan𝛼tan𝛽=3-431+3×43=13.答案:D【做一做2】sin75°的值为()A.ξ2-12B.ξ2+12C.ξ6-ξ24D.ξ6+ξ24解析:sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=ξ6+ξ24.答案:D-6-3.1.2两角和与差的正弦、余弦、正切公式ZHISHISHULI知识梳理ZHONGNANJVJIAO...