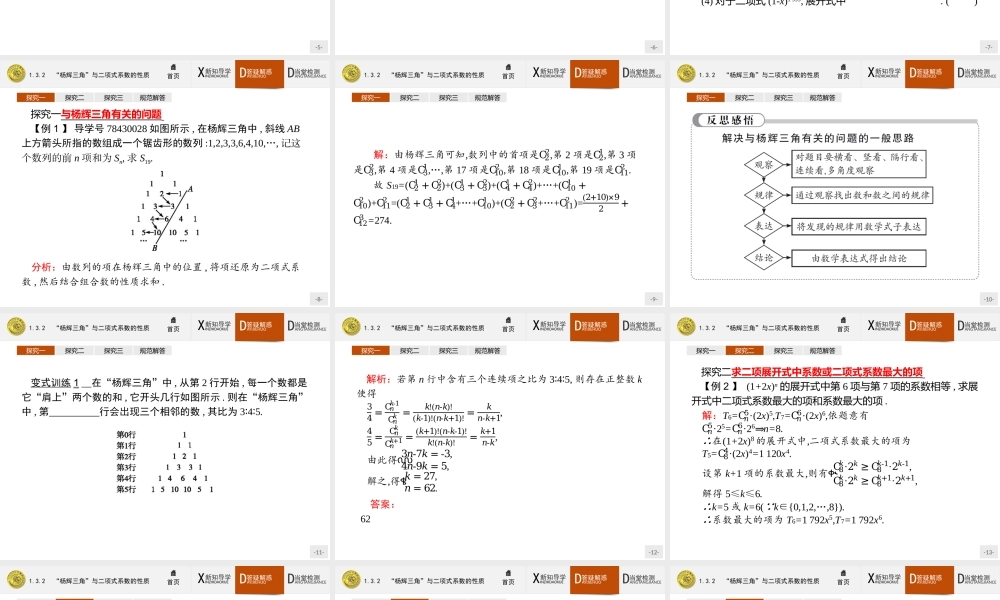
-1-1.3.2“杨辉三角”与二项式系数的性质-2-1.3.2“杨辉三角”与二项式系数的性质XINZHIDAOXUE新知导学DANGTANGJIANCE当堂检测DAYIJIEHUO答疑解惑首页学习目标思维脉络1.能认识杨辉三角,并能利用它写出(a+b)n的指数不是很大时的展开式.2.能记住二项式系数的性质,并能灵活运用性质解决相关问题.3.会用赋值法求展开式系数的和.-3-1.3.2“杨辉三角”与二项式系数的性质XINZHIDAOXUE新知导学DANGTANGJIANCE当堂检测DAYIJIEHUO答疑解惑首页1.杨辉三角(a+b)n展开式的二项式系数在当n取正整数时可以表示成如下形式:上面的二项式系数表称为“杨辉三角”.特点:(1)在同一行中,每行两端都是1,与这两个1等距离的项的系数相等.(2)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,即C𝑛+1𝑟=C𝑛𝑟-1+C𝑛𝑟.-4-1.3.2“杨辉三角”与二项式系数的性质XINZHIDAOXUE新知导学DANGTANGJIANCE当堂检测DAYIJIEHUO答疑解惑首页做一做1利用杨辉三角,将(a+b)7展开为.答案:a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7.2.二项式系数的性质(1)对称性.在(a+b)n的展开式中,与首末两端“等距离”的两个二项式系数相等,即(2)增减性与最大值.当k<时,二项式系数是逐渐增大的,由对称性知它的后半部分是逐渐减小的,且在中间取得最大值.当n是偶数时,中间的一项取得最大值;当n是奇数时,中间的两项相等,且同时取得最大值.(3)各二项式系数的和.C𝑛0=C𝑛𝑛,C𝑛1=C𝑛𝑛-1,…,C𝑛𝑟=C𝑛𝑛-𝑟.𝑛+12C𝑛𝑛-12和C𝑛𝑛+12C𝑛0+C𝑛1+C𝑛2+…+C𝑛𝑛=2n.-5-1.3.2“杨辉三角”与二项式系数的性质XINZHIDAOXUE新知导学DANGTANGJIANCE当堂检测DAYIJIEHUO答疑解惑首页做一做2在(a+b)8的展开式中,二项式系数最大的项为,在(a+b)9的展开式中,二项式系数最大的项为.解析:(a+b)8的展开式中有9项,所以中间一项的二项式系数最大,(a+b)9的展开式中有10项,所以中间两项的二项式系数最大,该项为C84a4b4=70a4b4.这两项分别为C94a5b4=126a5b4,C95a4b5=126a4b5.答案:70a4b4126a5b4与126a4b5-6-1.3.2“杨辉三角”与二项式系数的性质XINZHIDAOXUE新知导学DANGTANGJIANCE当堂检测DAYIJIEHUO答疑解惑首页做一做3A=的关系是()A.A>BB.A=BC.A