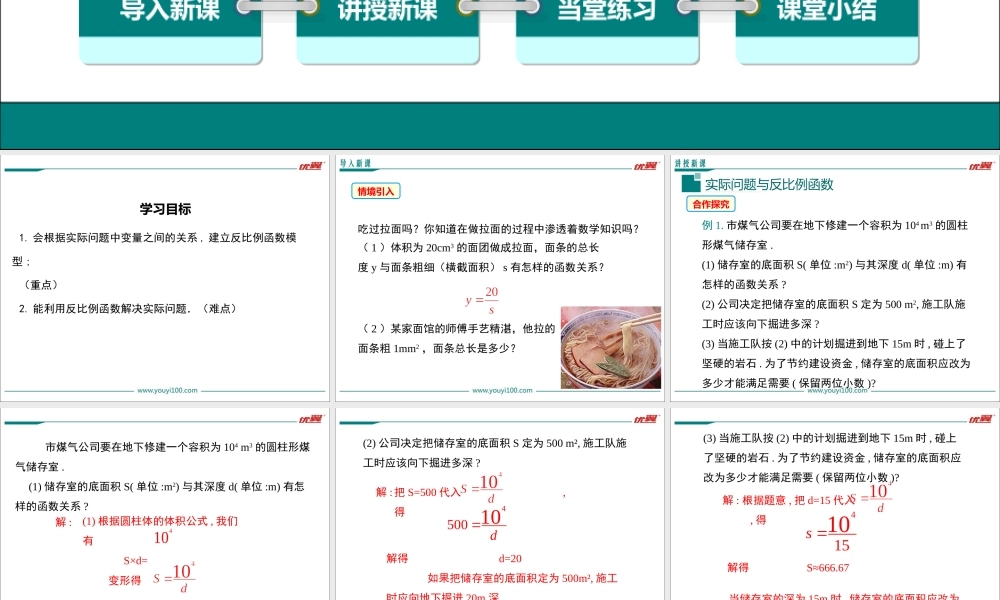
26.2实际问题与反比例函数第二十六章反比例函数优翼课件导入新课讲授新课当堂练习课堂小结学练优九年级数学下(RJ)教学课件第1课时实际问题中的反比例函数学习目标1.会根据实际问题中变量之间的关系,建立反比例函数模型;(重点)2.能利用反比例函数解决实际问题.(难点)吃过拉面吗?你知道在做拉面的过程中渗透着数学知识吗?(1)体积为20cm3的面团做成拉面,面条的总长度y与面条粗细(横截面积)s有怎样的函数关系?(2)某家面馆的师傅手艺精湛,他拉的面条粗1mm2,面条总长是多少?情境引入导入新课实际问题与反比例函数合作探究例1.市煤气公司要在地下修建一个容积为104m3的圆柱形煤气储存室.(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?(2)公司决定把储存室的底面积S定为500m2,施工队施工时应该向下掘进多深?(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要(保留两位小数)?讲授新课解:(1)根据圆柱体的体积公式,我们有S×d=410变形得即储存室的底面积S是其深度d的反比例函数.市煤气公司要在地下修建一个容积为104m3的圆柱形煤气储存室.(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?把S=500代入,得450010d解得d=20如果把储存室的底面积定为500m²,施工时应向地下掘进20m深.(2)公司决定把储存室的底面积S定为500m²,施工队施工时应该向下掘进多深?解:根据题意,把d=15代入,得41510s解得S≈666.67当储存室的深为15m时,储存室的底面积应改为666.67m²才能满足需要.(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要(保留两位小数)?解:圆柱体的体积公式是什么?第(2)问和第(3)问与过去所学的解分式方程和求代数式的值的问题有何联系?【反思小结】(1)问首先要弄清此题中各数量间的关系,容积为104,底面积是S,深度为d,满足基本公式:圆柱的体积=底面积×高,由题意知S是函数,d是自变量,改写后所得的函数关系式是反比例函数的形式.(2)问实际上是已知函数S的值,求自变量d的取值,(3)问则是与(2)相反.小组讨论我们学习过反比例函数,例如,当矩形面积一定时,长a是宽b的反比例函数,其函数解析式可以写为(S为常数,S≠0).请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数解析式.实例:;函数解析式...