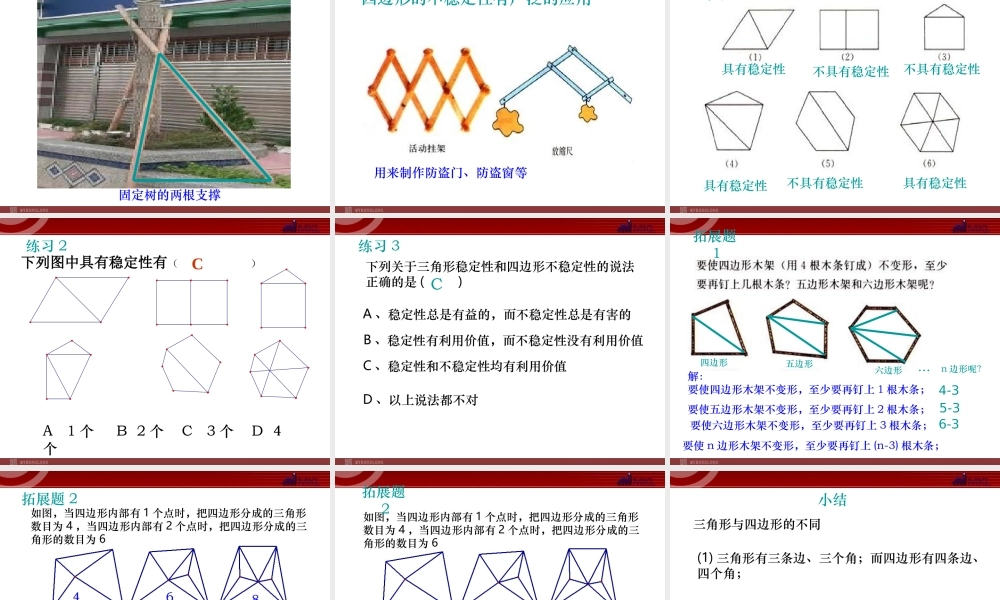
新人教版-八年级(上)数学-第十一章11.1.3三角形的稳定性一、学习目标1、了解三角形具有稳定性;2、学会利用三角形的稳定性解析一些实际问题;3、掌握三角形稳定性的意义;重点:了解三角形稳定性.难点:利用稳定性解析一些实际问题.二、重点和难点生活小常识探索与思考(1)将三根不条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?(2)将四根不条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?(3)在四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,它的形状会改变吗?三角形具有稳定性,四边形具有不稳定性结论三角形木架的形状不会改变,而四边形木架的形状会改变.用三根木棒钉一个三角形,你会发现再也无法改变这个三角形的形状和大小,也就是说,如果一个三角形的三条边固定了,那么三角形的形状和大小就完全确定了.在数学上把三角形的这个性质叫做三角形的稳定性.三角形的稳定性在生活中有广泛的应用,你能举出一些例子吗?三角形的性质---三角形的稳定性四边形不具有稳定性,人们往往通过改造,将其变成三角形从而增强其稳定性三角形的稳定性的应用三角形的稳定性的应用三角形的稳定性的应用三角形的稳定性的应用三角形的稳定性的应用房屋的人字架三角形的稳定性的应用照相机的三脚架三角形的稳定性的应用自行车三脚架三角形的稳定性的应用固定树的两根支撑四边形的不稳定性有广泛的应用用来制作防盗门、防盗窗等具有稳定性不具有稳定性不具有稳定性具有稳定性具有稳定性不具有稳定性练习1下列图形中哪些具有稳定性下列图中具有稳定性有()A1个B2个C3个D4个C练习2下列关于三角形稳定性和四边形不稳定性的说法正确的是()A、稳定性总是有益的,而不稳定性总是有害的B、稳定性有利用价值,而不稳定性没有利用价值C、稳定性和不稳定性均有利用价值D、以上说法都不对C练习3解:要使四边形木架不变形,至少要再钉上1根木条;要使五边形木架不变形,至少要再钉上2根木条;要使六边形木架不变形,至少要再钉上3根木条;要使n边形木架不变形,至少要再钉上(n-3)根木条;n边形呢?拓展题1四边形五边形六边形…4-35-36-3如图,当四边形内部有1个点时,把四边形分成的三角形数目为4,当四边形内部有2个点时,把四边形分成的三角形的数目为6(1)当四边形内部有3个点时,三角形的数目为___(2)当四边形内部有4个点时,三角形的数目为___(3)当四边形内部有n个点时,三角形的数目为_____8102n+2拓展题2212222232242...