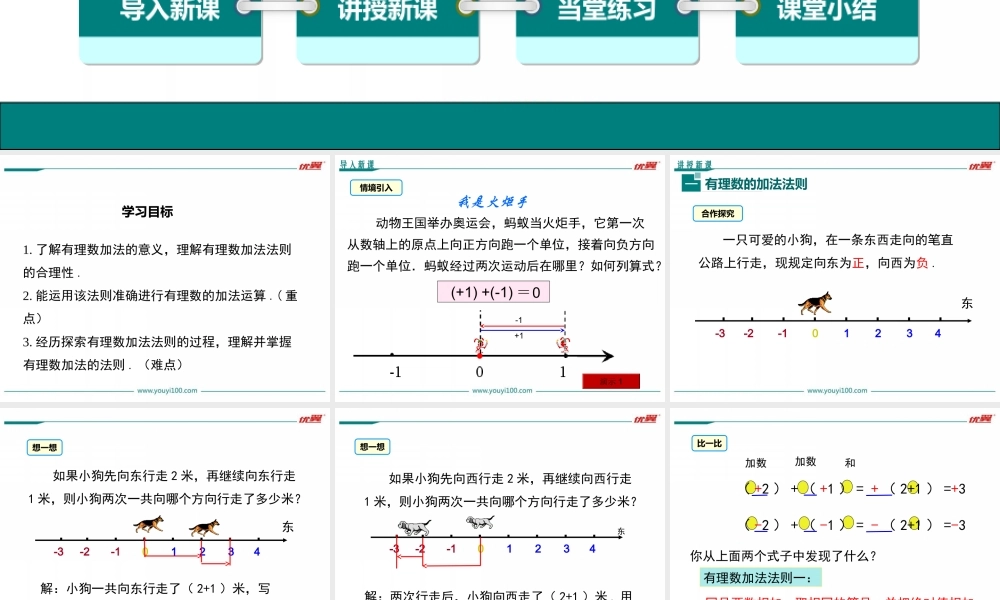
1.3有理数的加减法第一章有理数优翼课件导入新课讲授新课当堂练习课堂小结第1课时有理数的加法法则1.3.1有理数的加法七年级数学上(RJ)教学课件学习目标1.了解有理数加法的意义,理解有理数加法法则的合理性.2.能运用该法则准确进行有理数的加法运算.(重点)3.经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.(难点)我是火炬手演示1+1-1(+1)+(-1)=0动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?导入新课情境引入讲授新课有理数的加法法则一合作探究一只可爱的小狗,在一条东西走向的笔直公路上行走,现规定向东为正,向西为负.01234-1-2-3东如果小狗先向东行走2米,再继续向东行走1米,则小狗两次一共向哪个方向行走了多少米?01234-1-2-3东解:小狗一共向东行走了(2+1)米,写成算是为:(+2)+(+1)=+(2+1)(米)想一想如果小狗先向西行走2米,再继续向西行走1米,则小狗两次一共向哪个方向行走了多少米?01234-1-2-3东想一想解:两次行走后,小狗向西走了(2+1)米.用算式表示:(-2)+(-1)=-(2+1)(米)(+2)+(+1)=+(2+1)=+3(-2)+(-1)=-(2+1)=-3加数加数和你从上面两个式子中发现了什么?比一比同号两数相加,取相同的符号,并把绝对值相加.有理数加法法则一:(1)如果小狗先向西行走3米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?01234-1-3-2东小狗两次一共向西走了(3-2)米.用算式表示为:-3+(+2)=-(3-2)(米)想一想(2)如果小狗先向西行走2米,再继续向东行走3米,则小狗两次一共向哪个方向行走了多少米?01234-1-2东小狗两次一共向东走了(3-2)米.用算式表示为:-2+(+3)=+(3-2)(米)(3)如果小狗先向西行走2米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?01234-1-2东(-2)+(+2)=0(米)解:小狗一共行走了0米.写成算式为:-2+(+3)=+(3-2)-3+(+2)=-(3-2)-2+(+2)=(2-2)比一比加数加数和加数异号加数的绝对值不相等你从上面三个式子中发现了什么?有理数加法法则二:异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.如果小狗先向西行走3米,然后在原地休息,则小狗向哪个方向行走了多少米?01234-1-2东小狗向西行走了3米.写成算式为:(-3)+0=-3(米)想一想有理数加法法则...