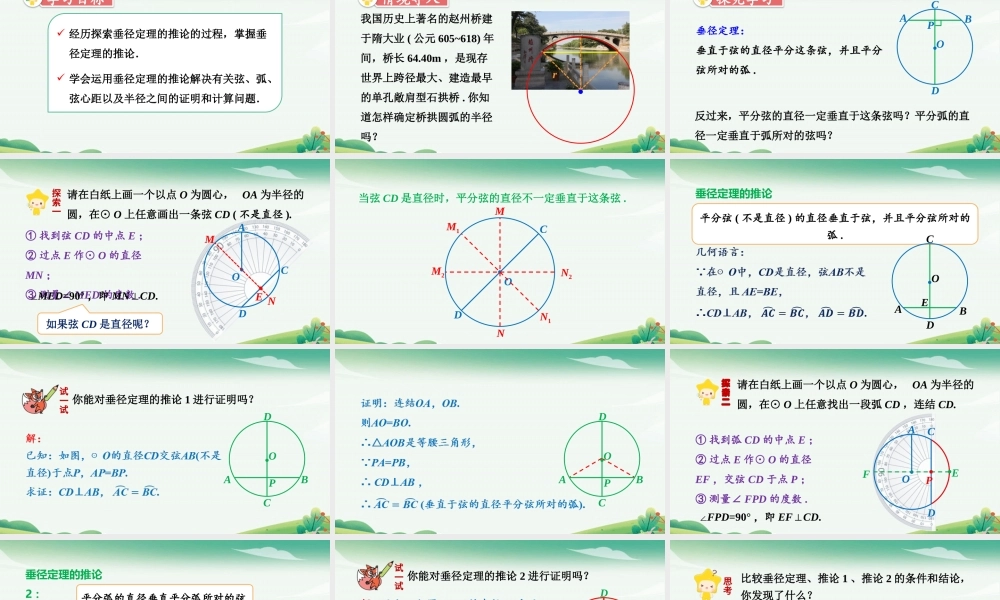
第3章圆的基本性质3.3垂径定理第2课时垂径定理(2)学习目标经历探索垂径定理的推论的过程,掌握垂径定理的推论.学会运用垂径定理的推论解决有关弦、弧、弦心距以及半径之间的证明和计算问题.情境导入我国历史上著名的赵州桥建于隋大业(公元605~618)年间,桥长64.40m,是现存世界上跨径最大、建造最早的单孔敞肩型石拱桥.你知道怎样确定桥拱圆弧的半径吗?·r探究学习垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.·CADBPO反过来,平分弦的直径一定垂直于这条弦吗?平分弧的直径一定垂直于弧所对的弦吗?请在白纸上画一个以点O为圆心,OA为半径的圆,在⊙O上任意画出一条弦CD(不是直径).探索一AOCD①找到弦CD的中点E;②过点E作⊙O的直径MN;③测量∠MED的度数.EMN∠MED=90°,即MN⊥CD.如果弦CD是直径呢?当弦CD是直径时,平分弦的直径不一定垂直于这条弦.OCDMNM1N1M2N2垂径定理的推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.·CADBEO你能对垂径定理的推论1进行证明吗?试一试·DACBPO·DACBPO请在白纸上画一个以点O为圆心,OA为半径的圆,在⊙O上任意找出一段弧CD,连结CD.AOCD①找到弧CD的中点E;②过点E作⊙O的直径EF,交弦CD于点P;③测量∠FPD的度数.∠FPD=90°,即EF⊥CD.EFP探索二垂径定理的推论2:平分弧的直径垂直平分弧所对的弦.·CADBEO你能对垂径定理的推论2进行证明吗?试一试·DACBPO所以点A与点B重合,即A,B关于直线CD对称,所以CD垂直平分弦AB,这就证明了推论2.思考比较垂径定理、推论1、推论2的条件和结论,你发现了什么?垂径定理及其推论可以看成由五个事项构成:①两条弦互相垂直;②一条弦经过圆心;③一条弦(不是直径)被平分;④平分弦所对的一条弧;⑤平分弦所对的另一条弧.这五个事项中,已知其中任意两个,必然能推出其余的三个.典例精讲例题已知赵州桥的跨径(桥拱圆弧所对的弦的长)为37.02m,拱高(桥拱圆弧的中点到弦的距离)为7.23m,求赵州桥的桥拱圆弧的半径(精确到0.1m).RABDOCRABDOC解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件.·ABOCDE随堂练习×1.判断下列说法是否正确.①垂直于弦的直线平分弦,并且平分弦所对的弧.()②弦所对的两弧中点的连线,垂直于弦,并且经过圆心.()③圆的不与直径垂直的弦必不被这条直径平分.()④平分弦的直径垂直于弦,并且平分弦所对的两条弧.()⑤圆内两条非直径的弦不能互相平分.()...