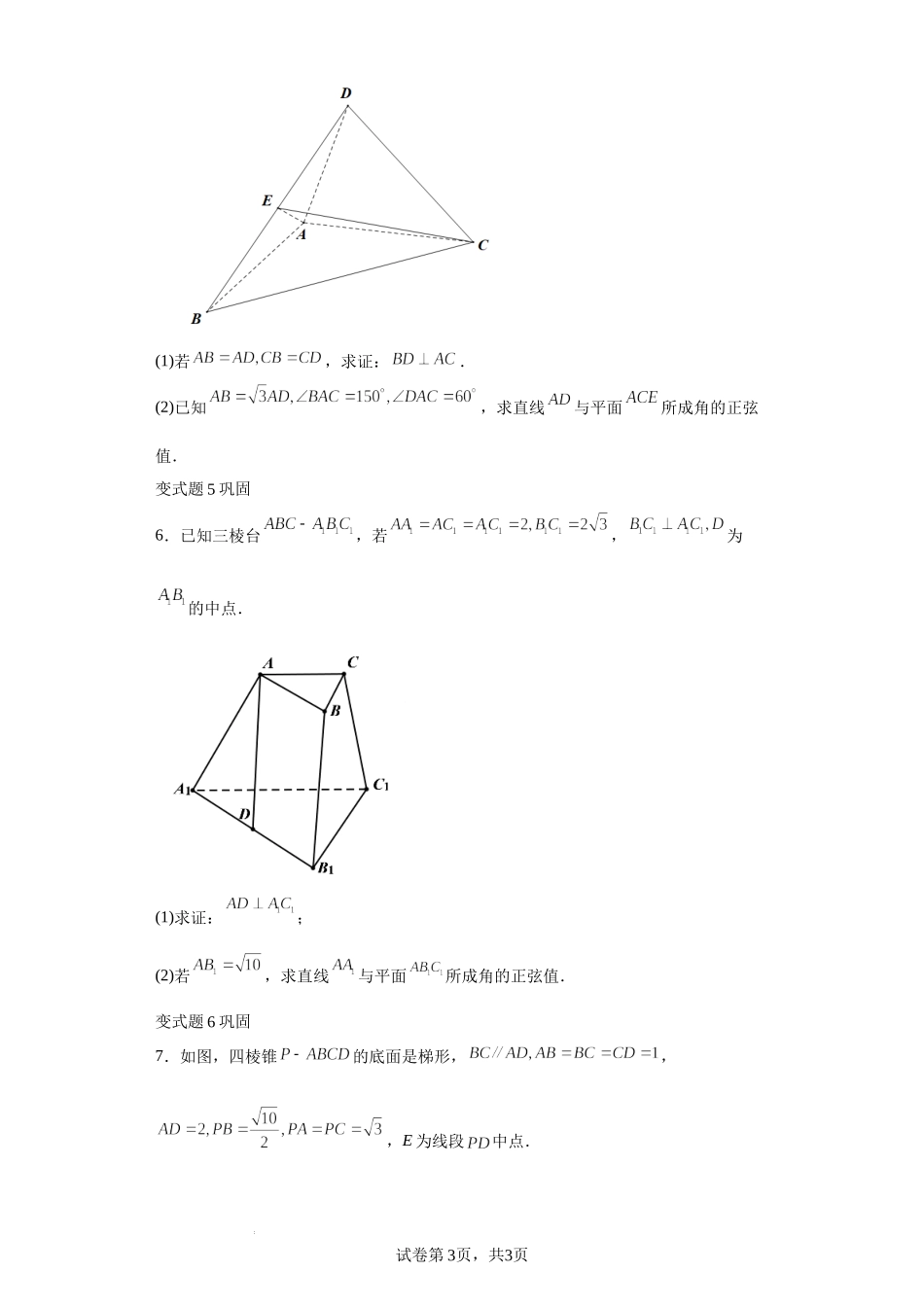
试卷第1页,共3页学科网(北京)股份有限公司学科网(北京)股份有限公司2022年高考浙江数学高考真题变式题19-22题原题191.如图,已知和都是直角梯形,,,,,,,二面角的平面角为.设M,N分别为的中点.(1)证明:;(2)求直线与平面所成角的正弦值.变式题1基础2.如图,在正三棱柱中,D为棱上的点,E,F,G分别为的中点,.(1)求证:;(2)求直线与平面所成角的大小;变式题2基础3.如图,在直角中,PO⊥OA,PO=2OA,将绕边PO旋转到的位置,使,得到圆锥的一部分,点C为的中点.试卷第2页,共3页(1)求证:;(2)设直线PC与平面PAB所成的角为,求.变式题3基础4.多面体如图所示,其中为等腰直角三角形,且.(1)求证:;(2)若,为的重心,平面,求直线与平面所成角的正弦值.变式题4基础5.如图,在三棱锥中,侧面底面,E为的中点,试卷第3页,共3页学科网(北京)股份有限公司学科网(北京)股份有限公司(1)若,求证:.(2)已知,求直线与平面所成角的正弦值.变式题5巩固6.已知三棱台,若,为的中点.(1)求证:;(2)若,求直线与平面所成角的正弦值.变式题6巩固7.如图,四棱锥的底面是梯形,,,E为线段中点.试卷第4页,共3页(1)证明:;(2)求直线与平面所成角的正弦值.变式题7巩固8.如图,四棱锥,底面ABCD为菱形,BD的中点为O,且PO⊥平面ABCD.(1)证明:;(2)若,,求直线PO与平面PAD所成角的正弦值.变式题8巩固9.已知空间几何体中,与均为等边三角形,平面平面,和平面所成的角为.(1)求证:;(2)若点E在平面上的射影落在的平分线上,求直线与平面所成角的正弦值.变式题9提升10.如图,在七面体中,四边形是菱形,其中,,试卷第5页,共3页学科网(北京)股份有限公司学科网(北京)股份有限公司,是等边三角形,且.(1)证明:;(2)求直线与平面所成角的正弦值.变式题10提升11.如图,在平面四边形中,,将沿翻折,使点到达点的位置,且平面平面.(1)证明:;(2)若为的中点,二面角的平面角等于,求直线PC与平面MCD所成角的正弦值.变式题11提升12.如图,已知直三棱柱,,,分别为线段,,的中点,为线段上的动点,,.试卷第6页,共3页(1)若,试证;(2)在(1)的条件下,当时,试确定动点的位置,使线段与平面所成角的正弦值最大.原题2013.已知等差数列的首项,公差.记的前n项和为.(1)若,求;(2)若对于每个,存在实数,使成等比数列,求d的取值范围.变式题1基础14.已知数列的前项和为,且满足.设,数列的前项和为.(1)证...