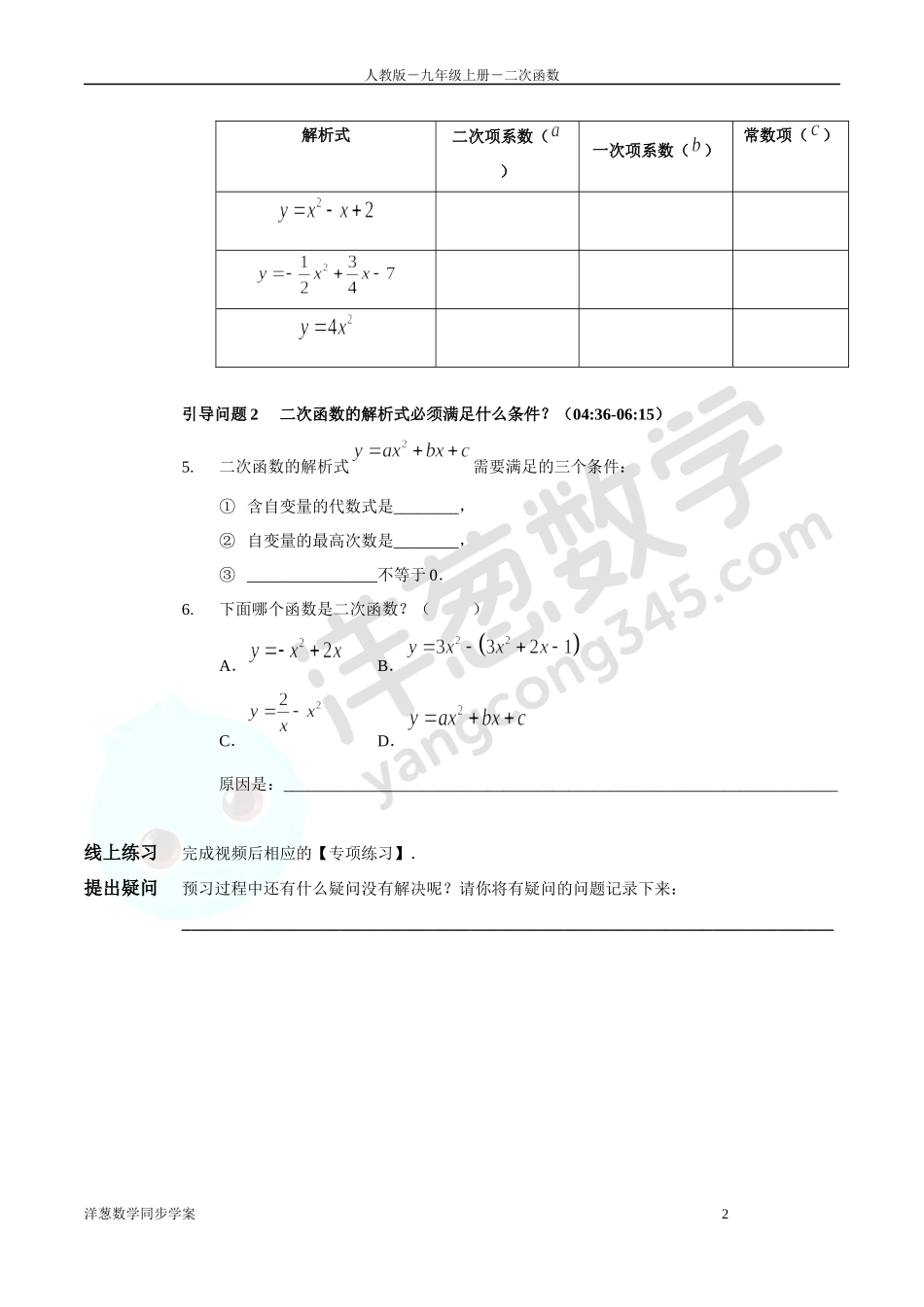
人教版-九年级上册-二次函数洋葱数学同步学案122.1二次函数的图象和性质22.1.1二次函数「引入课」二次函数的引入视频助学学习洋葱数学视频【二次函数的引入】「概念课」二次函数学习目标理解并掌握二次函数的定义理解并掌握二次函数解析式需要满足的条件能判断是否是二次函数的解析式视频助学请先思考引导问题,再看视频【二次函数】,然后完成引导问题下方的摘要填空.引导问题1什么是二次函数?二次函数的解析式有什么特点?(00:00-04:36)1.二次函数的定义:一般地,形如________________(、、为常数,________)的函数叫做二次函数.2.下列函数是二次函数的是().A.B.C.D.原因是:_____________________________________________________________________3.下面哪个函数不是二次函数?()A.B.C.D.原因是:_____________________________________________________________________4.请你完成下面的表格:扫码边看边学扫码边看边学人教版-九年级上册-二次函数洋葱数学同步学案2解析式二次项系数()一次项系数()常数项()引导问题2二次函数的解析式必须满足什么条件?(04:36-06:15)5.二次函数的解析式需要满足的三个条件:①含自变量的代数式是________,②自变量的最高次数是________,③________________不等于0.6.下面哪个函数是二次函数?()A.B.C.D.原因是:____________________________________________________________________线上练习完成视频后相应的【专项练习】.提出疑问预习过程中还有什么疑问没有解决呢?请你将有疑问的问题记录下来:______________________________________________________________________人教版-九年级上册-二次函数洋葱数学同步学案322.1.2二次函数的y=ax2图象和性质「概念课」二次函数的图象学习目标熟悉二次函数的图象,并能根据图象掌握二次函数的性质视频助学请先思考引导问题,再看视频【二次函数图象】,然后完成引导问题下方的摘要填空.引导问题1二次函数的图象有什么特点?(00:00-04:51)1.使用描点法在右面的坐标系中画出二次函数的图象,请根据图象回答下列问题.(1)二次函数的图象是一条________________(2)右图中二次函数的图象有什么特征:________________(3)这个函数开口向________,函数图象的顶点是最________点,图象顶点的坐标是________________引导问题2什么是二次函数的最值?二次函数的增减性是怎样变化的?(04:51-07:21)2.二次...