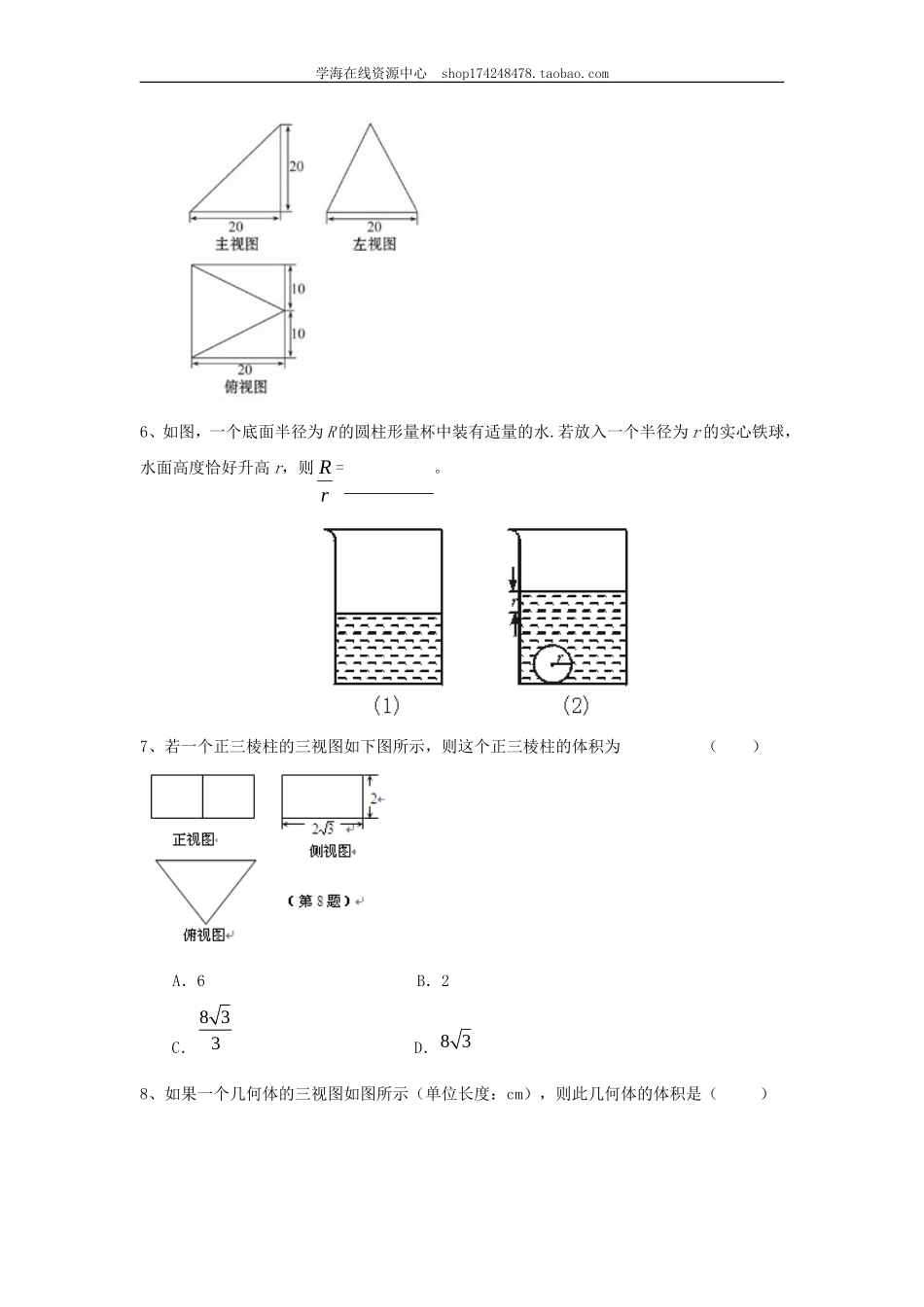
学海在线资源中心shop174248478.taobao.com【巩固练习】1、若正方体的棱长为2,则以该正方体各个面的中心为顶点的凸多面体的体积为()(A)26(B)23(C)33(D)232、圆柱的侧面展开图是一个边长为6π和4π的矩形,则该圆柱的底面积是()(A)24π2(B)36π2(C)36π2或16π2(D)9π或4π3、如图,某几何体的主视图与左视图都是边长为1的正方形,且体积为,则该几何体的俯视图可以是()4、如图是一几何体的三视图,其左视图是等腰直角三角形,则其表面积为()A.262B.244C.246D.125、已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是()学海在线资源中心shop174248478.taobao.com6、如图,一个底面半径为R的圆柱形量杯中装有适量的水.若放入一个半径为r的实心铁球,水面高度恰好升高r,则rR=。7、若一个正三棱柱的三视图如下图所示,则这个正三棱柱的体积为()A.6B.2C.833D.838、如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的体积是()学海在线资源中心shop174248478.taobao.comA.396cmB.380cmC.380162cmD.3224cm39.(2015北京高考)某三棱锥的三视图如图所示,则该三棱锥的表面积是()A.2+B.4+C.2+2D.510、如图为一个几何体的三视图,左视图和主视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积为()(A)6(B)12(C)24(D)3211.(2015东城区模拟)已知某个几何体的三视图如图所示(正视图弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是cm3.学海在线资源中心shop174248478.taobao.com12、直三棱柱111ABCABC的各顶点都在同一球面上,若12ABACAA,120BAC,则此球的表面积等于。13、如图是一个几何体的三视图,该几何体的体积为8,则a的值为______.14.(2015德阳模拟)一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点).(1)求证:MN∥平面CDEF;(2)求多面体ACDEF﹣的体积.学海在线资源中心shop174248478.taobao.com15、四面体的六条棱中,有五条棱长都等于a.(1)求该四面体的体积的最大值;(2)当四面体的体积最大时,求其表面积.【参考答案与解析】1、【答案】B.【解析】由题意知以正方体各个面的中心为顶点的凸多面体为正八面体(即两个同底同高同棱长的正四棱锥),所有棱长均为1,其中每个正四棱锥的高均为22,故正八面体的体积为21222=21=323VV正四棱锥,故选B.2、【答案】D.【解析】由题意...