知识讲解_ 不等式的全章复习与巩固_提高.doc

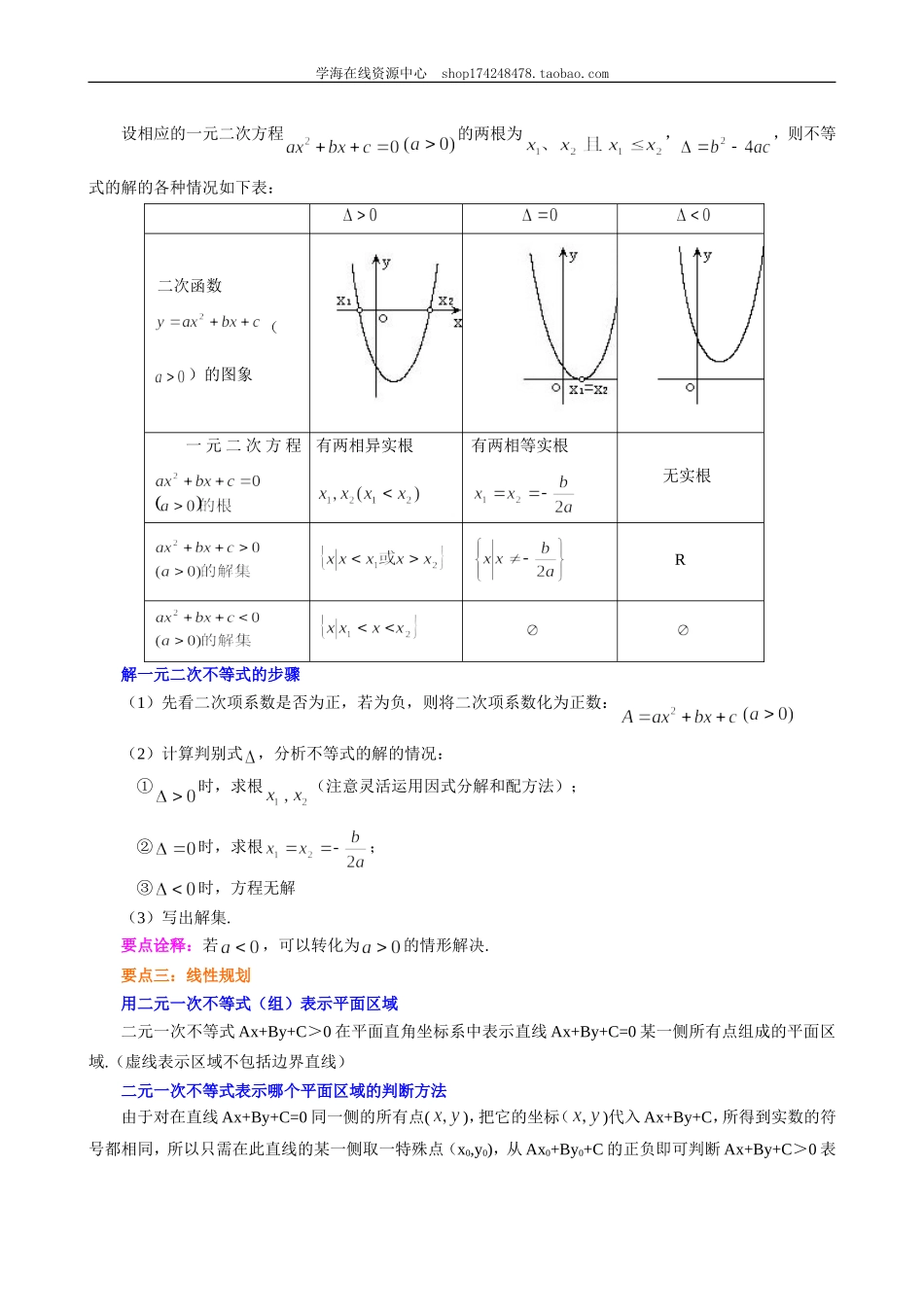
学海在线资源中心 《不等式》全章复习与巩固 编稿：李霞 审稿：张林娟 【学习目标】 1.能正确的记忆和灵活运用不等式的性质； 2.会从实际情境中抽象出一元二次不等式模型和二元一次不等式组，提高数学建模能力； 3.掌握一元二次方程，二次函数，一元二次不等式，这三个“二次”的联系，会解一元二次不等式； 4.了解二元一次不等式的几何意义，能用平面区域表示二元一次不等式组，会从实际情境中抽象出一些简单的二元线性规划问题，并能加以解决； 5.会用基本不等式解决简单的最大（小）值问题，注意基本不等式适用的条件. 【知识网络】 不等式 不等关系与不等式 一元二次不等式及其解法 二元一次不等式（组）与平面区域 基本不等式 最大（小）值问题 简单的线性规划 【要点梳理】 要点一：不等式的主要性质 (1)对称性： (2)传递性： (3)加法法则：； (4)乘法法则：； ， (5) 乘方法则： (6) 开方法则： 要点诠释：不等式性质中要注意等价双向推出和单向推出关系的不同. 要点二：三个“二次”的关系 一元二次不等式或的解集： 设相应的一元二次方程的两根为，，则不等式的解的各种情况如下表： 二次函数（）的图象 一元二次方程 有两相异实根 有两相等实根 无实根 R 解一元二次不等式的步骤 （1）先看二次项系数是否为正，若为负，则将二次项系数化为正数： （2）计算判别式，分析不等式的解的情况： ①时，求根（注意灵活运用因式分解和配方法）； ②时，求根； ③时，方程无解 （3）写出解集. 要点诠释：若，可以转化为的情形解决. 要点三：线性规划 用二元一次不等式（组）表示平面区域 二元一次不等式Ax+By+C＞0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.（虚线表示区域不包括边界直线） 二元一次不等式表示哪个平面区域的判断方法 由于对在直线Ax+By+C=0同一侧的所有点()，把它的坐标（)代入Ax+By+C，所得到实数的符号都相同，所以只需在此直线的某一侧取一特殊点（x0,y0)，从Ax0+By0+C的正负即可判断Ax+By+C＞0表示直线哪一侧的平面区域.（特殊地，当C≠0时，常把原点作为此特殊点） 线性规划的有关概念： ①线性约束条件： 如果两个变量、满足一组一次不等式组，则称不等式组是变量、的约束条件，这组约束条件都是关于、的一次不等式，故又称线性约束条件． ②线性目标函数： 关于x、y的一次式z=ax+by(a，b∈R)是欲达到最大值或最小值所涉及的变量x、y的解析式，叫线性目标函数． ③线性规划问题： 一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题． ④可行解、可行域和最优解： 在线性规划问题中，满足线性约束条件的解（x,y）叫可行解．由所有可行解组成的集合叫做可行域． 使目标函数取得最大或最小值的可行解叫线性规划问题的最优解． 要点诠释：求线性目标函数在线性约束条件下的最优解的步骤 （1）设变量，建立线性约束条件及线性目标函数； （2) 由二元一次不等式表示的平面区域做出可行域； （3)求出线性目标函数在可行域内的最值(即最优解)； （4)作答． 要点四：基本不等式 两个重要不等式 ①，那么（当且仅当时取等号“=”）； ②基本不等式：如果是正数，那么（当且仅当时取等号“=”）. 算术平均数和几何平均数 算术平均数：称为的算术平均数； 几何平均数：称为的几何平均数； 因此基本不等式可叙述为：两个正数的算术平均数不小于它们的几何平均数. 基本不等式的应用 ,且（定值），那么当时，有最小值； ,且（定值），那么当时，有最大值. 要点诠释 ：在用基本不等式求函数的最值时，应具备的三个条件 ① 一正：函数的解析式中，各项均为正数； ② 二定：函数的解析式中，含变数的各项的和或积必须有一个为定值； ③ 三取等：函数的解析式中，含变数的各项均相等，取得最值. 几个常用变形不等式： ①（当且仅当a=b时等号成立）； ②（a+b）2≥4ab（当且仅当a=b时等号成立）； ③；特别地：； ④ . 【典型例题】 类型一：不等式的性质 例1．若为实数，则下列结论中正确的是（ ） A. 若，则或 B. 若，则或 C. 若或，则 D. 若或，则 【思路点拨】利用不等式的性质，逐项进行判断. 【解析】若，则同号. 当时，由得； 当时，由得. 所以A项正确，B项错误. 由得，即，所以或 同理，由得或 显然C项不正确. 同理D项也不正确. 【总结升华】解答此类问题应注意一下几个方面： （1）准确理解不等式的性质； （2）掌握作差法比较大小这种最基本的方法； （3）了解符号的运算规律； （4）灵活利用特殊数值对结论进行检验. 举一反三： 【变式1】已知求证。 【答案】因为，所以ab>0，. 于是 ，即 由c<0 ，得 【变式2】已知，则成立的一个充要条件是（ ） A. B. C. D. 【答案】C 例2．已知函数,满足,,那么的取值范围是 . 【思路点拨】将用及表示出来，再利用不等式性质求得正确的范围. 【解析】 解法一：方程思想(换元)： 由 ，求得 ∴ 又 ∴ ， 即。 解法二：待定系数法 设f(3)=9a-c=mf(1)+nf(2)=m(a-c)+n(4a-c) 解法三：数形结合(线性规划) 所确定区域如图： 设，将边界点(0,1)(3,7)代入即求出. 【总结升华】利用几个不等式的范围来确定某个不等式的范围是一类常见的综合问题，对于这类问题要注意：“同向（异向）不等式的两边可以相加（相减）”，这种转化不是等价变形，在一个解题过程中多次使用这种转化时，就有可能扩大真实的取值范围，解题时务必小心谨慎，先建立待求范围的整体与已知范围的整体的等量关系，最后通过“一次性不等关系的运算，求得待求的范围”，是避免犯错误的一条途径. 举一反三： 【变式】已知，，求的取值范围。 【答案】[-3，10] 类型二：不等式的求解 例3．已知函数的值域为，若关于的不等式的解集为，则实数的值为_______. 【解析】的值域为， ，， 又的解集为，， ， . 【总结升华】解决本题的关键是（1）准确把握一元二次不等式的解法；（2）掌握一元二次不等式的解集、一元二次方程的根与一元二次函数的零点三者之间的关系，根据需要进行彼此的互化. 【高清课堂：不等式综合392606 例2】 例4． 已知关于x的方程的两根为，试问是否存在实数m，使得不等式 对任意实数a∈[－1,1]及l∈[－1,1]恒成立？若存在，求m的取值范围；若不存在，说明理由． 【总结升华】 ①在含参不等式问题中，二次不等式恒成立的充要条件的理论依据: ax2+bx+c>0对任何xR恒成立a>0且Δ=b2-4ac<0； ax2+bx+c<0对任何xR恒成立a<0且Δ=b2-4ac<0。 ②与不等式恒成立相互依存,相互支撑与相互转化的最值命题： μ＜f(x)恒成立μ＜f(x)的最小值 μ＞f(x)恒成立μ＞f(x)的最大值 举一反三： 【变式】在R上定义运算：xy=x(1-y),若不等式（x-a）(x+a)<1对任意实数x成立，则（ ） A．-1<a<1 B. 0<a<2 C. D. 【答案】由所给定义（x-a） (x+a)<1对任意xR成立 （x-a）(1-x-a)<1对xR恒成立 x2-x+(1-a2+a)>0对xR恒成立 Δ=1-4（1-a2+a）<0 4a2-4a-3<0 故应选C 【变式2】若对于任意xR恒有3x2+2x+2>m（x2+x+1）,求m的值 【答案】对任意xR 恒有3x2+2x+2>m（x2+x+1）成立 对任意xR 恒（3-m）x2+(2-m)x+(2-m)>0成立 又因mN*，∴m=1 类型三：二元一次方程（组）与平面区域 例5．不等式组表示的平面区域的面积为　　（　） 2x + y – 6= 0 = 5 x＋y – 3 = 0 O y x A B C M y =2 A．4 　 B.1　 C.5　 D.无穷大 【答案】B 【解析】如图，作出可行域，△ABC的面积即为所求，由梯形OMBC的面积减去梯形OMAC的面积即可. 【总结升华】正确的画出可行域是解决这类问题的关键. 举一反三： 【变式】不等式组在xy平面上的解的集合为（ ） A．四边形内部 B. 三角形內部 C.一点 D.空集 【答案】B 类型四：求线性目标函数在线性约束条件下的最优解 例6．(2015 福建)变量x，y满足约束条件，若z=2x-y的最大值为2，则实数m等于( ) A．-2 B．-1 C．1 D．2 【思路点拨】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得m的值。 【答案】C 【解析】 将目标函数变形为y=2x-z，当z取最大值，则直线纵截距最小，故当m≤0时，不满足题意；当m＞0时，画出可行域，如图所示， 其中．显然O(0，0)不是最优解，故只能是最优解，代入目标函数得，解得m=1， 故选C． 【总结升华】注意线性规划问题的求解步骤，含有参数的问题注意变化的范围，多结合图形解决问题. 举一反三： 【变式1】 (2015 湖北)若变量x，y满足约束条件 则3x+y的最大值是_________． 【答案】首先根据题意所给的约束条件画出其表示的平面区域如下图所示，然后根据图像可得: 目标函数z=3x+y过点B（3，1）取得最大值，即zmax=3×3+1=10，故应填10. 【变式 2】某饼店制作的豆沙月饼每个成本35元，售价50元；凤梨月饼每个成本20元，售价30元。现在要将这两种月饼装成一盒，个数不超过10个，售价不超过350元，问豆沙月饼与凤梨月饼各放几个，可使利润最大？又最大利润为多少？ 【答案】设一盒內放入x个豆沙月饼，y个凤梨月饼，利润为z元 则x，y必须满足， 目标函数为z＝15x＋10y 在可行区內的顶点附近z＝f ( x，y ) 的最大值， 所以，一盒内装2个豆沙月饼8个凤梨月饼或4个豆沙月饼5个凤梨月饼，可得最大利润110元。 类型五：均值不等式求最值及应用 例7．已知正数满足，试求、的范围。 【思路点拨】利用均值不等式化归为其它不等式的求解或者转化为函数最值的求解. 【解析】 解法一： 由， 则， 即 解得， 当且仅当即时取“=”号，故的取值范围是. 又 解得， 当且仅当即时取“=”号，故的取值范围是 解法二： 由，知， 则，由，则： ， 当且仅当，并求得时取“=”号， 故的取值范围是。 ， 当且仅当，并求得时取“=”号， 故的取值范围是。 【总结升华】利用均值不等式求函数的最值，除了抓住均值不等式的使用条件“一正、二定、三相等”外，还要灵活变换函数式，配凑均值不等式，并正确应用均值不等式求解函数最值问题. 举一反三： 【变式1】（2016 海南校级模拟）设均为正数，且，则的最小值为（ ） A.1 B. 3 C. 6 D. 9 【答案】 均为正数，且， ，整理可得 由基本不等式可得 整理可得 解得 ，或（舍去） ，当且仅当时取等号，故选：D 【变式2】（1）设a,b,c是RtΔABC的三边，c为斜边之长，且a+b+c=4,试求C的取值范围； （2）设三个数a,b,c成等比数列，且a+b+c=1，试求b的取值范围。 【答案】（1）由已知得c2=a2+b2 ① 4-c=a+b ② a,bR+且满足2（a2+b2）≥(a+b)2 ③ ∴将①，②代入③得2c2≥(4-c)2 ④ ∵a+b>c a+b+c>2c 又a+b+c=4 ∴c<2 ⑤ 于是由④、⑤得 ∴所求C的取值范围为 （2）由已知得b2=ac ① 1-b=a+c ② 由题设知a、c同号 （i）当a,c同为正数时，(当且仅当a=c时等号成立) ∴由①得a+c≥2|b| ∴再由②得1-b≥2|b|2|b|+b≤1 ③ ∴若b>0，则由③得； 若b<0， 则由③得 -1≤b<0 ∴由③解得-1≤b<0或 (ii)当a,c 同为负数时， ④ ∴由②、④得1-b≤-2|b|2|b|-b≤-1，无解 于是综合（i）（ii）得所求b的取值范围为[-1，0）∪（0， ] 例8．求函数的最小值. 【思路点拨】是二项“和”的形式，但其“积”的形式不为定值. 而可与相约，即其积为定积1，因此可以先添、减项6，即，再用均值不等式. 【解析】， 　　当且仅当，即时,等号成立. 所以的最小值是. 　　【总结升华】为了创造条件利用均值不等式，添项是常用的一种变形技巧；为了保证式子的值不变，添项后一定要再减去同一项. 举一反三： 【变式1】求的最大值. 【答案】且为常数 （当且仅当时取等号） ∴当时，. 【变式2】已知，且满足，求的最大值. 【答案】 当且仅当，即时等号成立。所以的最大值为 例9．为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C(单位：万元)与隔热层厚度x(单位：cm)满足关系：(0≤x≤10)，若不建隔热层，每年能源消耗费用为8万元．设为隔热层建造费用与20年的能源消耗费用之和． (1)求k的值及的表达式； (2)隔热层修建多厚时，总费用达到最小，并求最小值． 【思路点拨】(1)由题意知C(0)＝8，代入的表达式即可求出k的值，求的表达式时需注意定义域；(2)利用均值不等式即可求解． 【解析】(1)设隔热层厚度为x cm，由题设，每年能源消耗费用为C(x)＝，再由C(0)＝8，得k＝40，因此． 而建造费用为． 最后得隔热层建造费用与20年的能源消耗费用之和为 (0≤x≤10)． (2)． 当且仅当，即x＝5时取“＝”所以当隔热层修建5 cm厚时，总费用达到最小值70万元． 【总结升华】利用不等式的性质解决实际应用题，首先，要仔细阅读题目，弄清要解决的实际问题，确定是求什么量的最值(即题中的y)；其次，分析题目中给出的条件，建立y与x的函数关系式(x一般为题目中最后所要求的量)；最后，利用不等式的有关知识解题． 举一反三： 【变式1】建造一个容积为8m3，深为2m的长方体无盖水池，如果池底和池壁的造价分别为每平方米120元和80元，那么水池的最低造价为 元. 【答案】设水池池底的一边长为xm，则另一边长为， 则总造价y为： （元） 当且仅当即时，y取最小值为1760. 所以水池的最低造价为1760元. 【变式2】某汽车运输公司购买了一批豪华大客车投入营运，据市场分析每辆客车营运的总利润y (单位：10万元)与营运年数x(x∈N+)为二次函数关系(如下图所示)，则每辆客车营运的年平均利润最大时，营运了( ) A．3年 B．4年 C．5年 D．6年 【答案】由题图可得，营运总利润，则营运的平均利润， ∵ x∈N+， ∴ ， 当且仅当，即x＝5时取“＝”． ∴ x＝5时营运的年平均利润最大． 故选C.