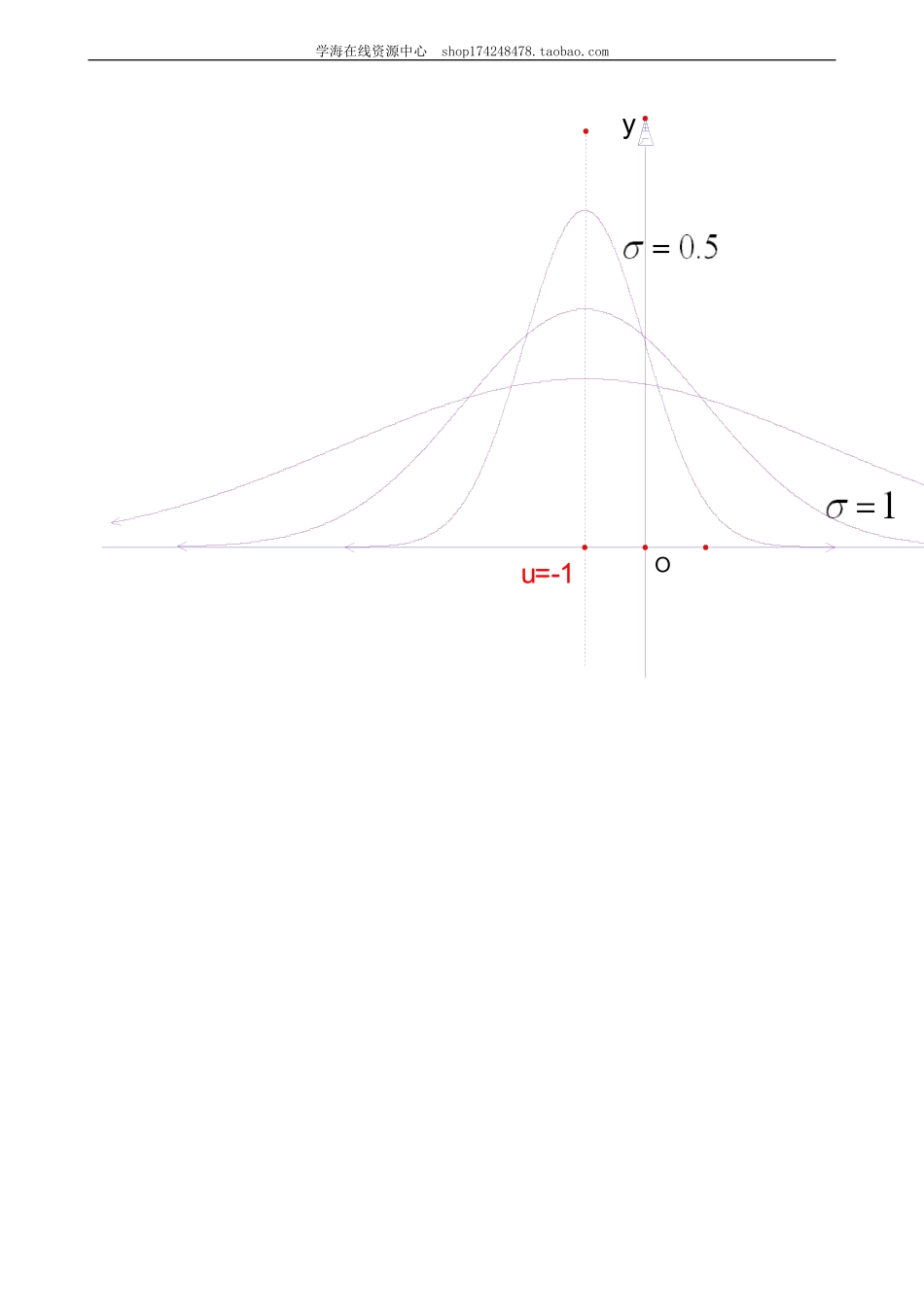
学海在线资源中心shop174248478.taobao.com正态分布编稿:赵雷审稿:李霞【学习目标】1.了解正态分布曲线的特点及曲线所表示的意义。2.了解正态曲线与正态分布的性质。【要点梳理】要点诠释:要点一、概率密度曲线与概率密度函数1.概念:对于连续型随机变量X,位于x轴上方,X落在任一区间(a,b]内的概率等于它与x轴、直线xa与直线xb所围成的曲边梯形的面积(如图阴影部分),这条概率曲线叫做X的概率密度曲线,以其作为图象的函数()fx叫做X的概率密度函数。2、性质:①概率密度函数所取的每个值均是非负的。②夹于概率密度的曲线与x轴之间的“平面图形”的面积为1③()PaXb的值等于由直线xa,xb与概率密度曲线、x轴所围成的“平面图形”的面积。要点二、正态分布1.正态变量的概率密度函数正态变量的概率密度函数表达式为:22()2,1()(R)2xxex,(0,)其中x是随机变量的取值;μ为正态变量的期望;是正态变量的标准差.2.正态分布(1)定义如果对于任何实数,()abab随机变量X满足:,()()baPaXbxdx,则称随机变量X服从正态分布。记为2(,)XN。(2)正态分布的期望与方差若2(,)XN,则X的期望与方差分别为:EX,2DX。要点诠释:(1)正态分布由参数和确定。参数是均值,它是反映随机变量取值的平均水平的特征数,可用样本的均值去估计。是学海在线资源中心shop174248478.taobao.com标准差,它是衡量随机变量总体波动大小的特征数,可以用样本的标准差去估计。(2)经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.要点三、正态曲线及其性质:1.正态曲线如果随机变量X的概率密度函数为22()21()(R)2xfxex,其中实数和为参数(0,),则称函数()fx的图象为正态分布密度曲线,简称正态曲线。u=0Oy学海在线资源中心shop174248478.taobao.comu=-1Oy学海在线资源中心shop174248478.taobao.comu=1Oy...