初中数学竞赛精品标准教程及练习62：绝对值.docVIP免费

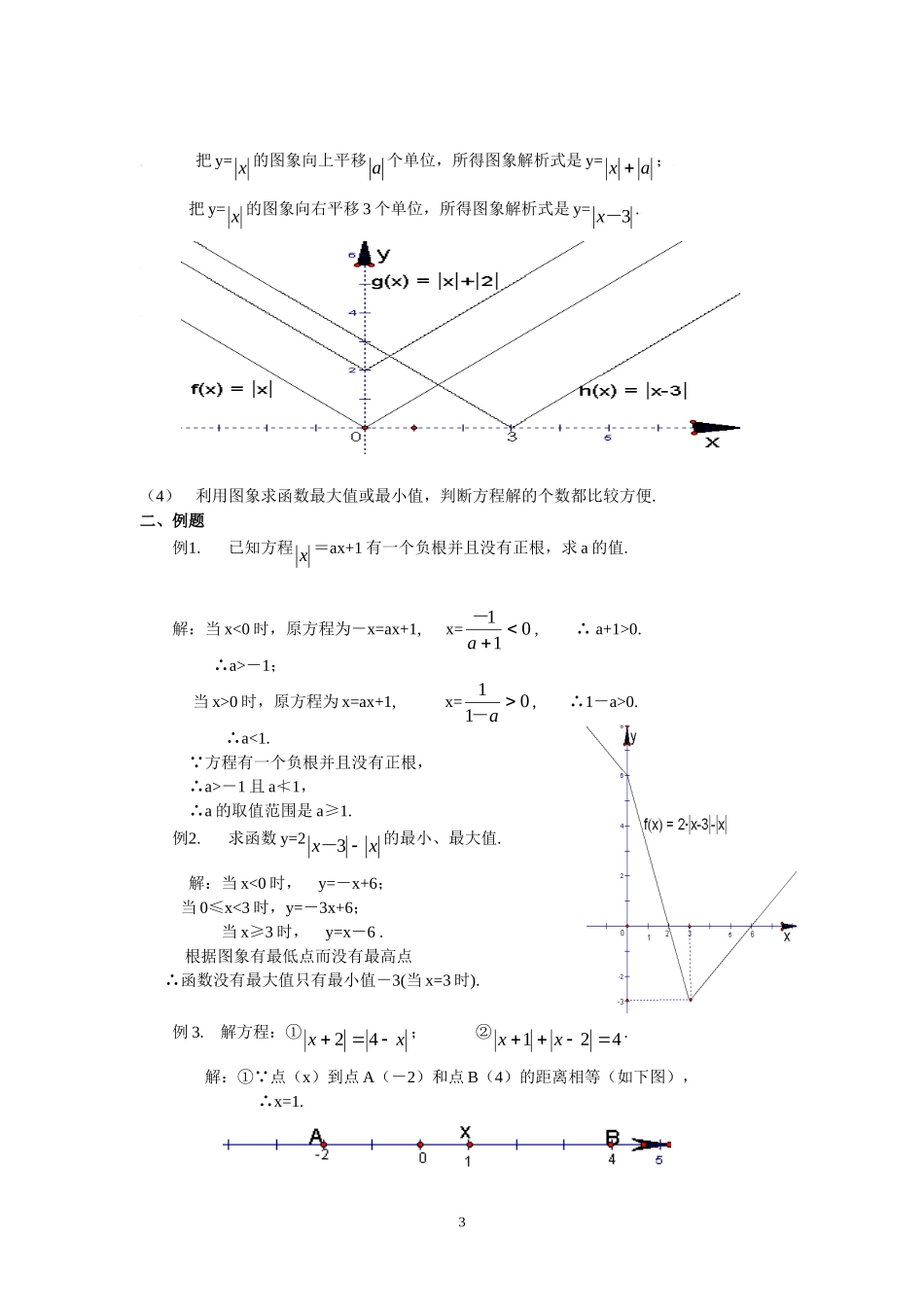
初中数学竞赛精品标准教程及练习（62）绝对值一、内容提要1.绝对值的定义：正数的绝对值是它本身，负数的绝对值是它的相反数，零的绝对值是零.用式子表示如下：)0(0)0()0(aaaaaa2.初中阶段学习含绝对值符号的代数式化简，方程、不等式的解法，以及函数作图等.解答时，一般是根据定义先化去绝对值符号，这时关健是按已知条件判断绝对值符号内的式子的值是正或是负，若含有变量的代数式，不能确定其正、负时，则采取零点分区讨论法.例如：（1）化简)2(xx解：当x=0,x=2时,)2(xx=0；当x<0或x>2时,)2(xx=x(x－2)=x2－2x；当02时，x=4.∴原方程的解是：x=－2，x=4..（3）作函数y=2xx的图象.解：化去绝对值符号，得y=－2x+2(x<0)；y=2(0≤x≤2)；y=2x－2(x>2).分别作出上述三个函数的图象（如图），就是函数y=2xx的图象.3.绝对值的几何意义是：在数轴上一个数的绝对值，就是表示这个数的点离开原点的距离.用这一定义，在解含绝对值符号的方程、不等式时，常可用观察法.例如：①解方程3x；②解不等式3x；③解不等式32＋x.解：① 3x的几何意义是：x是数轴上到原点的距离等于3个单位的点所表示的数，即3和－3，102X<002∴方程3x的解是x=3,x=－3.② 3x的几何意义是：x是数轴上到原点的距离小于3个单位的点所表示的数，∴不等式3x的解集是－3＜x＜3.③ 2x的零点是x=－2,∴32＋x的几何意义是：x是数轴上到点（－2）的距离大于3个单位的点所表示的数，∴32＋x的解集是x<－5或x>1.（如下图）4.绝对值的简单性质：①绝对值是非负数；②两个互为相反数，它们的绝对值相等.根据这些性质，可简化函数的作图步骤.例如：（1）对整个函数都在绝对值符号内时，可先作出不含绝对值符号的图象，再把横轴下方的部份，绕x轴向上翻折作函数图象：①y=1x②y=22xx（2）当f（－x）=f(x),图象关于纵轴对称，这时可先作当x<0时函数图象，再画出关于纵轴对称的图象.例如：y=x2－2x－3的图象，可先作y=x2+2x－3自变量x<0时的图象（左半图）再画右半图（与左半图关于纵轴对称）.21-20--5（3）把y=x的图象向上平移a个单位，所得图象解析式是y=ax；把y=x的图象向右平移3个单位，所得图象解析式是y=3－x.（4）利用图象求函数最大值或最小值，判断方程解的个数都比较方便.二、例题例1.已知方程x＝ax+1有一...