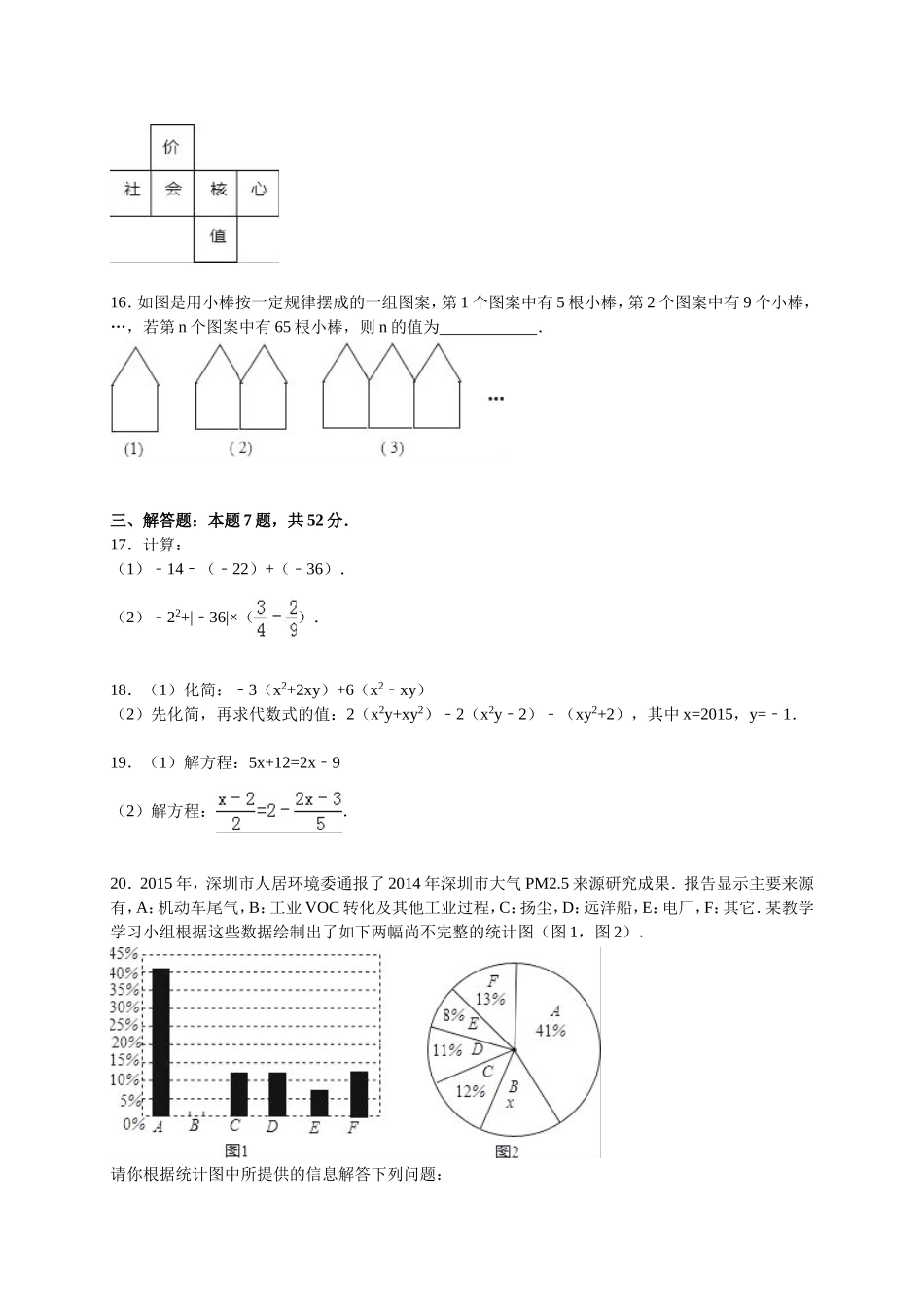
七年级上学期期末数学试卷一、选择题:本题共12小题,每小题3分,共36分.每小题有四个选项,其中只有一个是正确的.1.6的相反数是()A.6B.﹣6C.D.﹣2.如图所示的几何体是由一些小立方块搭成的,则这个几何体的左视图是()A.B.C.D.3.在2015年深圳高交会上展出了现实版“钢铁侠”战衣﹣﹣马丁飞行喷射包,可连续飞行30分钟,载重120公斤,其网上预售价为160万元,数据160万元用科学记数法表示为()A.1.6×104元B.1.6×105元C.1.6×106元D.0.16×107元4.如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为()A.过一点有无数条直线B.两点之间线段的长度,叫做这两点之间的距离C.两点确定一条直线D.两点之间,线段最短5.小明每个月收集废电池a个,小亮比小明多收集20%,则小亮每个月收集的废电池数为()A.(a+20%)个B.a(1+20%)个C.个D.个6.当前,“低头族”已成为热门话题之一,小颖为了解路边行人步行边低头看手机的情况,她应采用的收集数据的方式是()A.对学校的同学发放问卷进行调查B.对在路边行走的学生随机发放问卷进行调查C.对在路边行走的行人随机发放问卷进行调查D.对在图书馆里看书的人发放问卷进行调查7.如图,下列表示角的方法中,不正确的是()A.∠AB.∠EC.∠αD.∠18.若x=3是方程ax+2x=14a﹣的解,则a的值为()A.10B.5C.4D.29.小亮为表示出2015年他们家在“生活开支”项目的变化情况,他应该采用的统计图是()A.折线统计图B.条形统计图C.扇形统计图D.以上均可以10.当x的值变大时,代数式﹣2x+3的值()A.变小B.不变C.变大D.无法确定11.下列各式一定成立的是()A.﹣B.|a|=a﹣C.(﹣a)3=a3D.(﹣a)2=a212.把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、B、D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数是()A.60°B.67.5°C.75°D.85°二、填空题:每小题3分,共12分.请把答案填在答题卷相应的表格里.13.如果节约20元记作+20元,那么浪费10元记作元.14.若3am+3bn+2与﹣2a5b是同类项,则mn=.15.一个正方体的每个面都有一个汉字,其平面展开图如图所示,那么在该正方体中与“价”字相对的字是.16.如图是用小棒按一定规律摆成的一组图案,第1个图案中有5根小棒,第2个图案中有9个小棒,…,若第n个图案中有65根小棒,则n的值为.三、解答题:本题7题,共52分.17....