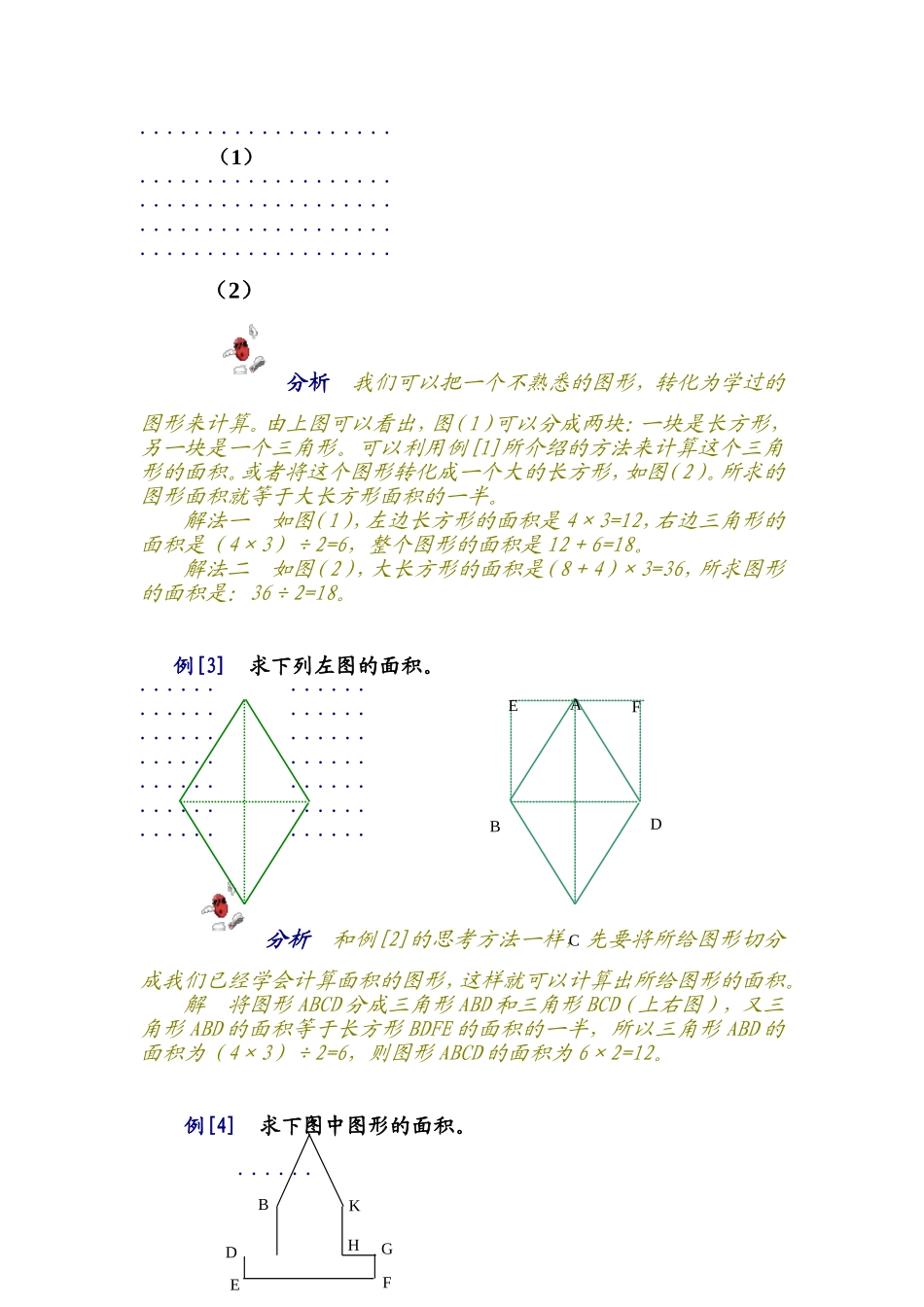
第六讲格点与面积在一张方格图中,每个方格都是一个小正方形,并且大小都相等,我们称为一个面积单位。例如:右图中带阴影的小方格就是一个面积单位。借助格点图,我们可以很快的比较或计算图形的面积大小。典型例题例[1]下图是用皮筋在钉板上分别围成的正方形、长方形、平行四边形和三角形。它们的面积分别是多少?·······························································································(1)(2)(3)(4)分析题中所给的几个图形都是规则图形,它们的面积可以运用公式求得。而要运用公式,首先要结合点子图计算出有关的边长和高。解图(1)是正方形,边长是2,它的面积是2×2=4。图(2)是长方形,长是4,宽是2,它的面积是4×2=8。图(3)是平行四边形,从平行四边形的左边移动一个直角三角形到右边,使得平行四边形变成一个长方形,所求的面积是3×2=6。图(4)是三角形,将三角形扩展成一个长方形。三角形ABC的面积是长方形AFBC面积的一半,三角形ACD的面积是长方形ACDE面积的一半,所以三角形ABD的面积是(3×2)÷2=6÷2=3例[2]求下图中各图的面积。·························································FCBEFDA···················(1)············································································(2)分析我们可以把一个不熟悉的图形,转化为学过的图形来计算。由上图可以看出,图(1)可以分成两块:一块是长方形,另一块是一个三角形。可以利用例[1]所介绍的方法来计算这个三角形的面积。或者将这个图形转化成一个大的长方形,如图(2)。所求的图形面积就等于大长方形面积的一半。解法一如图(1),左边长方形的面积是4×3=12,右边三角形的面积是(4×3)÷2=6,整个图形的面积是12+6=18。解法二如图(2),大长方形的面积是(8+4)×3=36,所求图形的面积是:36÷2=18。例[3]求下列左图的面积。····················································································分析和例[2]的思考方法一样,...