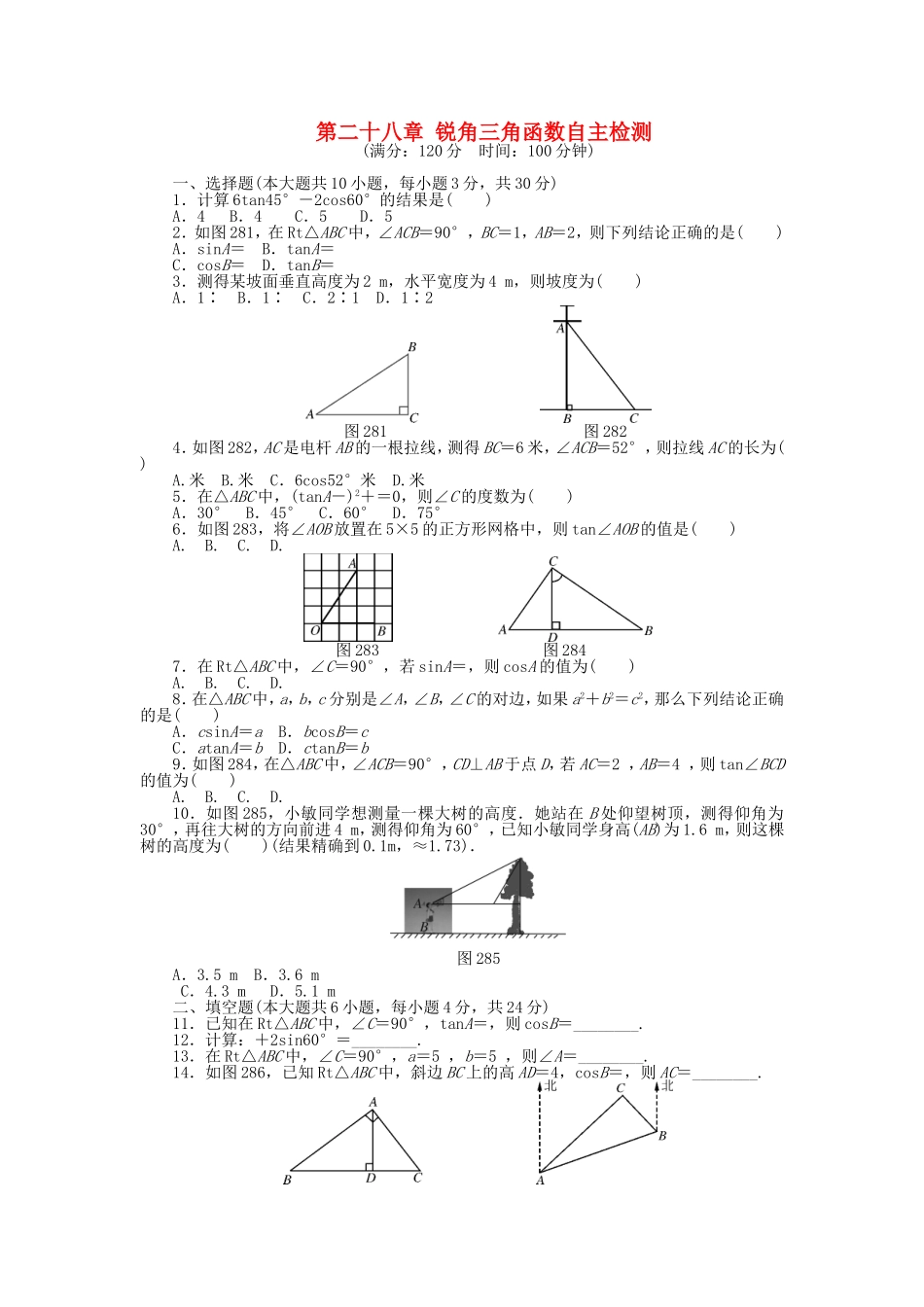
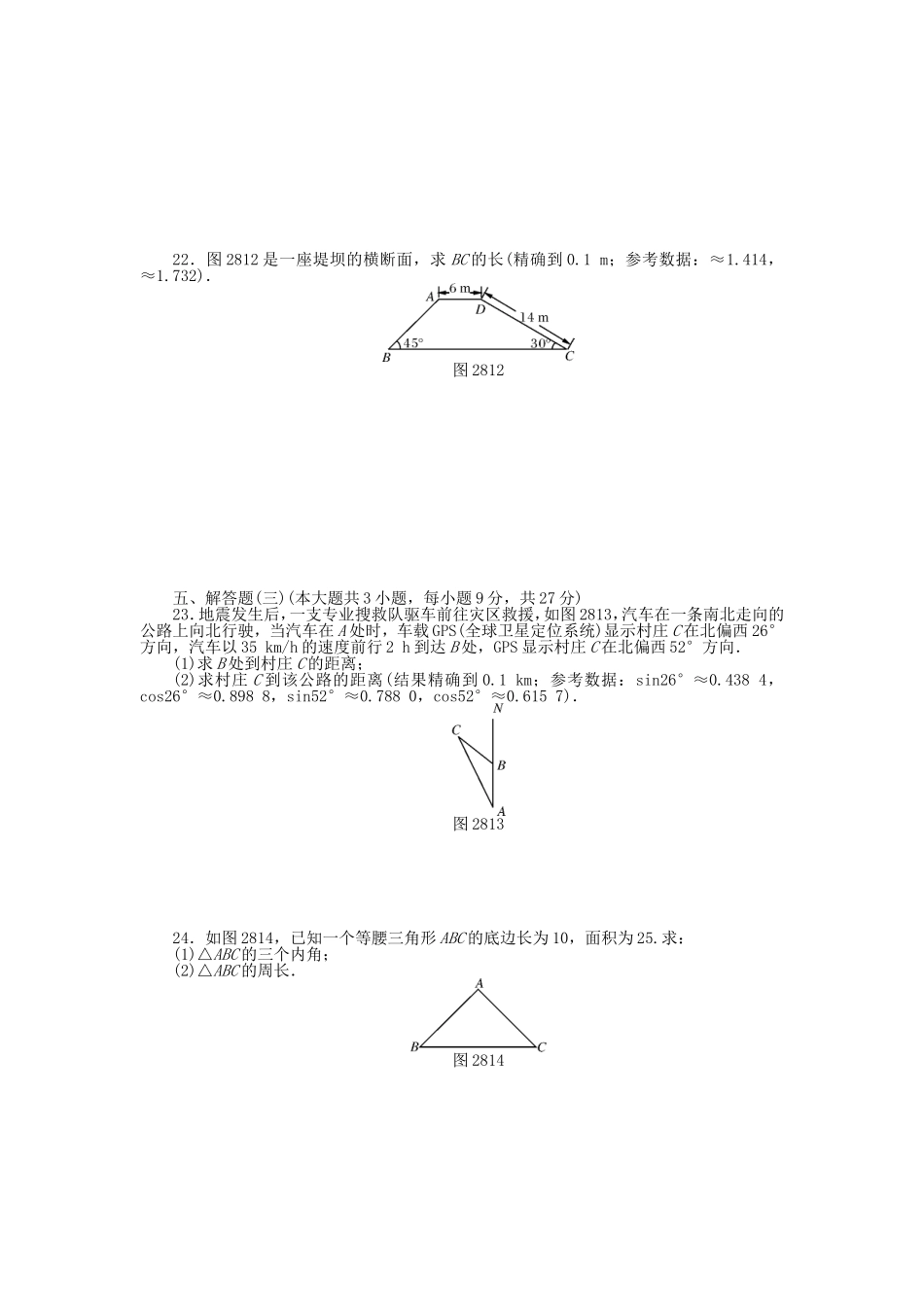
第二十八章锐角三角函数自主检测(满分:120分时间:100分钟)一、选择题(本大题共10小题,每小题3分,共30分)1.计算6tan45°-2cos60°的结果是()A.4B.4C.5D.52.如图281,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是()A.sinA=B.tanA=C.cosB=D.tanB=3.测得某坡面垂直高度为2m,水平宽度为4m,则坡度为()A.1∶B.1∶C.2∶1D.1∶2图281图2824.如图282,AC是电杆AB的一根拉线,测得BC=6米,∠ACB=52°,则拉线AC的长为()A.米B.米C.6cos52°米D.米5.在△ABC中,(tanA-)2+=0,则∠C的度数为()A.30°B.45°C.60°D.75°6.如图283,将∠AOB放置在5×5的正方形网格中,则tan∠AOB的值是()A.B.C.D.图283图2847.在Rt△ABC中,∠C=90°,若sinA=,则cosA的值为()A.B.C.D.8.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是()A.csinA=aB.bcosB=cC.atanA=bD.ctanB=b9.如图284,在△ABC中,∠ACB=90°,CD⊥AB于点D,若AC=2,AB=4,则tan∠BCD的值为()A.B.C.D.10.如图285,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高(AB)为1.6m,则这棵树的高度为()(结果精确到0.1m,≈1.73).图285A.3.5mB.3.6mC.4.3mD.5.1m二、填空题(本大题共6小题,每小题4分,共24分)11.已知在Rt△ABC中,∠C=90°,tanA=,则cosB=________.12.计算:+2sin60°=________.13.在Rt△ABC中,∠C=90°,a=5,b=5,则∠A=________.14.如图286,已知Rt△ABC中,斜边BC上的高AD=4,cosB=,则AC=________.图286图28715.如图287,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB=________.16.若方程x2-4x+3=0的两根分别是Rt△ABC的两条边,若△ABC最小的角为A,那么tanA=______.三、解答题(一)(本大题共3小题,每小题6分,共18分)17.计算:+-1-2cos60°+(2-π)0.18.如图288,某河堤的横断面是梯形ABCD,BC∥AD,迎水坡AB长13米,且tan∠BAE=,求河堤的高BE.图28819.如图289,在△ABC中,AD⊥BC,tanB=cos∠CAD.求证:AC=BD.图289四、解答题(二)(本大题共3小题,每小题7分,共21分)20.如图2810,在鱼塘两侧有两棵树A,B,小华要测量此两树之间的距离,他在距A树30m的C处测得∠ACB=30°,又在B处测得∠ABC=120°.求A,B两树之间的距...