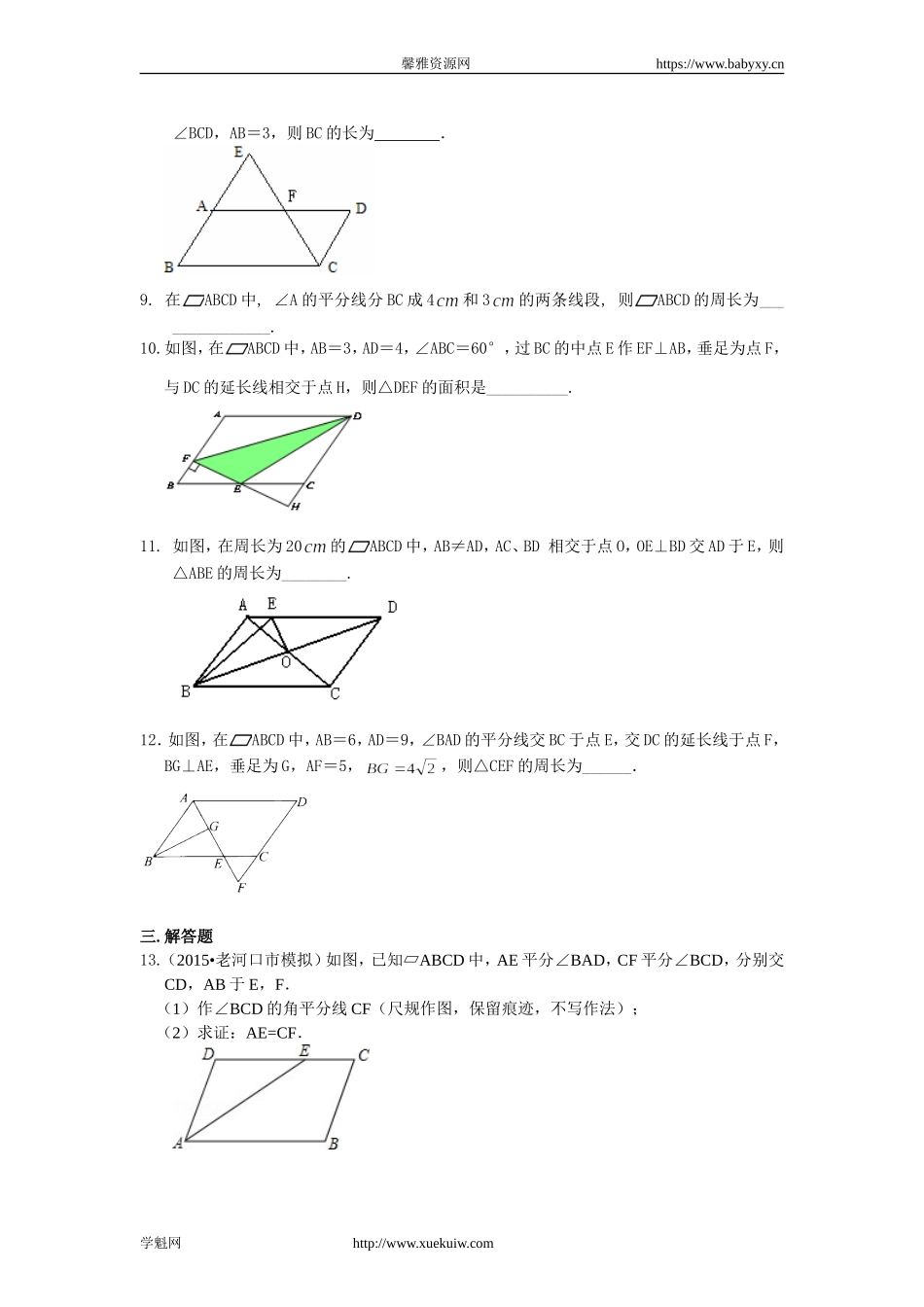
馨雅资源网https://www.babyxy.cn【巩固练习】一.选择题1.平行四边形一边长12,那么它的两条对角线的长度可能是().A.8和16B.10和16C.8和14D.8和122.以不共线的三点A、B、C为顶点的平行四边形共有()个.A.1B.2C.3D.无数3.平行四边形两邻边分别为24和16,若两长边间的距离为8,则两短边间的距离为().A.5B.6C.8D.124.国家级历史文化名城--金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是()A.红花,绿花种植面积一定相等B.紫花,橙花种植面积一定相等C.红花,蓝花种植面积一定相等D.蓝花,黄花种植面积一定相等5.(2015•应城市二模)如图,口ABCD的周长为20cm,AC与BD相交于点O,OEAC⊥交AD于E,则△CDE的周长为()A.6cmB.8cmC.10cmD.12cm6.在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为()A.2B.C.D.15二.填空题7.(2015春•监利县期末)已知直线ab∥,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为.8.如图,在ABCD中,E是BA延长线上一点,AB=AE,连结EC交AD于点F,若CF平分学魁网http://www.xuekuiw.com馨雅资源网https://www.babyxy.cn∠BCD,AB=3,则BC的长为.9.在ABCD中,∠A的平分线分BC成4和3的两条线段,则ABCD的周长为_______________.10.如图,在ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是__________.11.如图,在周长为20的ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为________.12.如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AF=5,,则△CEF的周长为______.三.解答题13.(2015•老河口市模拟)如图,已知▱ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F.(1)作∠BCD的角平分线CF(尺规作图,保留痕迹,不写作法);(2)求证:AE=CF.学魁网http://www.xuekuiw.com馨雅资源网https://www.babyxy.cn14.如图,过平行四边形ABCD内任一点P作各边的平行线分别交AB、BC、CD、DA于E、F、G、H.求证:S平行四边形ABCD-S平行四边形AEPH=2S△AFG.15.如图,四边形ABCD是平行四边...