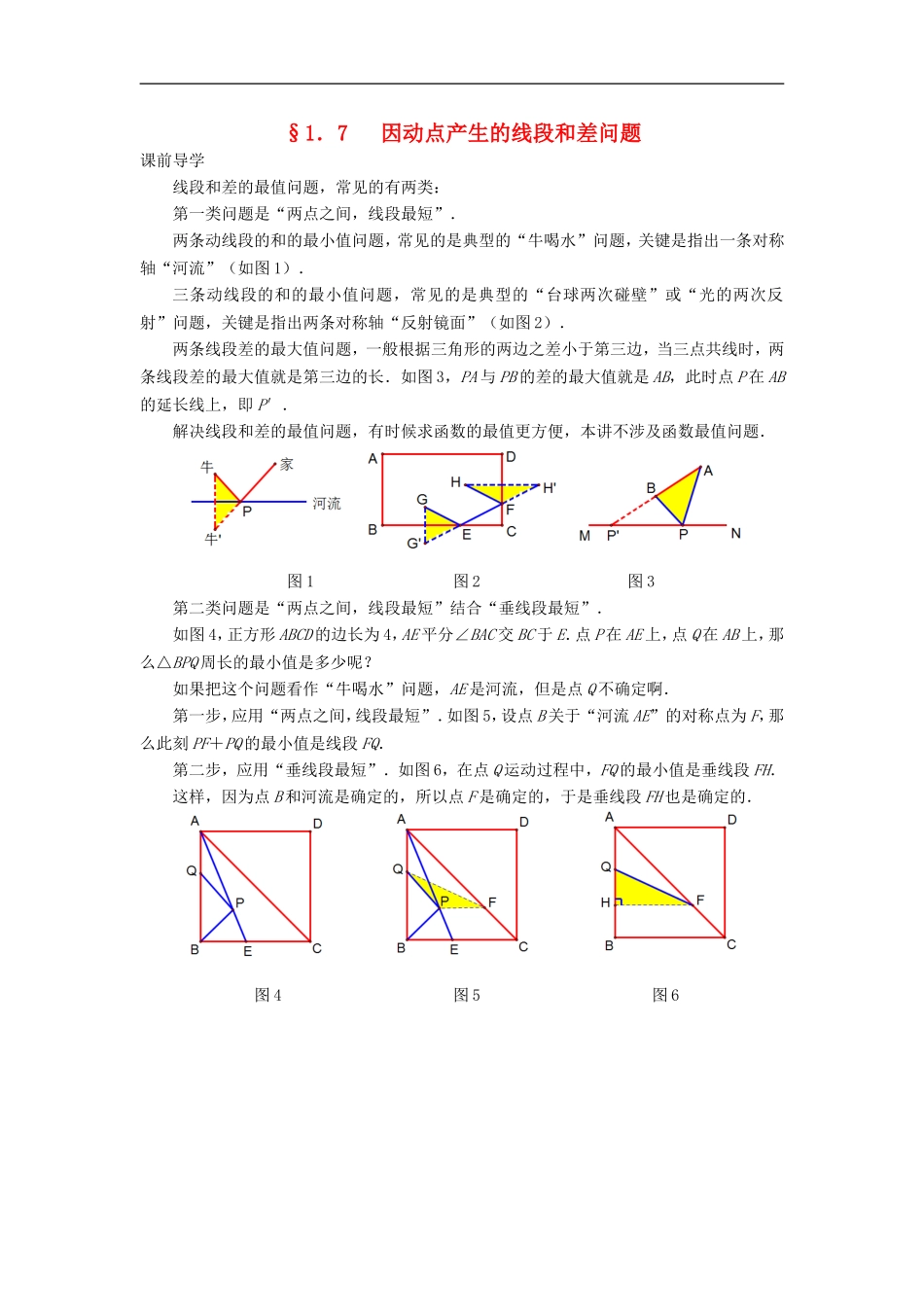
§1.7因动点产生的线段和差问题课前导学线段和差的最值问题,常见的有两类:第一类问题是“两点之间,线段最短”.两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,PA与PB的差的最大值就是AB,此时点P在AB的延长线上,即P′.解决线段和差的最值问题,有时候求函数的最值更方便,本讲不涉及函数最值问题.图1图2图3第二类问题是“两点之间,线段最短”结合“垂线段最短”.如图4,正方形ABCD的边长为4,AE平分∠BAC交BC于E.点P在AE上,点Q在AB上,那么△BPQ周长的最小值是多少呢?如果把这个问题看作“牛喝水”问题,AE是河流,但是点Q不确定啊.第一步,应用“两点之间,线段最短”.如图5,设点B关于“河流AE”的对称点为F,那么此刻PF+PQ的最小值是线段FQ.第二步,应用“垂线段最短”.如图6,在点Q运动过程中,FQ的最小值是垂线段FH.这样,因为点B和河流是确定的,所以点F是确定的,于是垂线段FH也是确定的.图4图5图6例502014年湖南省郴州市中考第26题已知抛物线y=ax2+bx+c经过A(-1,0)、B(2,0)、C(0,2)三点.(1)求这条抛物线的解析式;(2)如图1,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标;(3)如图2,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.图1图2动感体验请打开几何画板文件名“14郴州26”,拖动点P运动,可以体验到,当点P运动到CB的中点的正上方时,四边形ABPC的面积最大.拖动点G运动,可以体验到,当A、G、M三点共线时,GC+GM最小,△CMG的周长最小.思路点拨1.设交点式求抛物线的解析式比较简便.2.连结OP,把四边形ABPC的面积分割为三个三角形的面积和.3.第(3)题先用几何说理确定点G的位置,再用代数计算求解点G的坐标.图文解析(1)因为抛物线与x轴交于A(-1,0)、B(2,0)两点,设y=a(x+1)(x-2).代入点C(0,2),可得a=-1.所以这条抛物线的解析式为y=-(x+1)(x-2)=-x2+x+2.(2)如图3,连结OP....