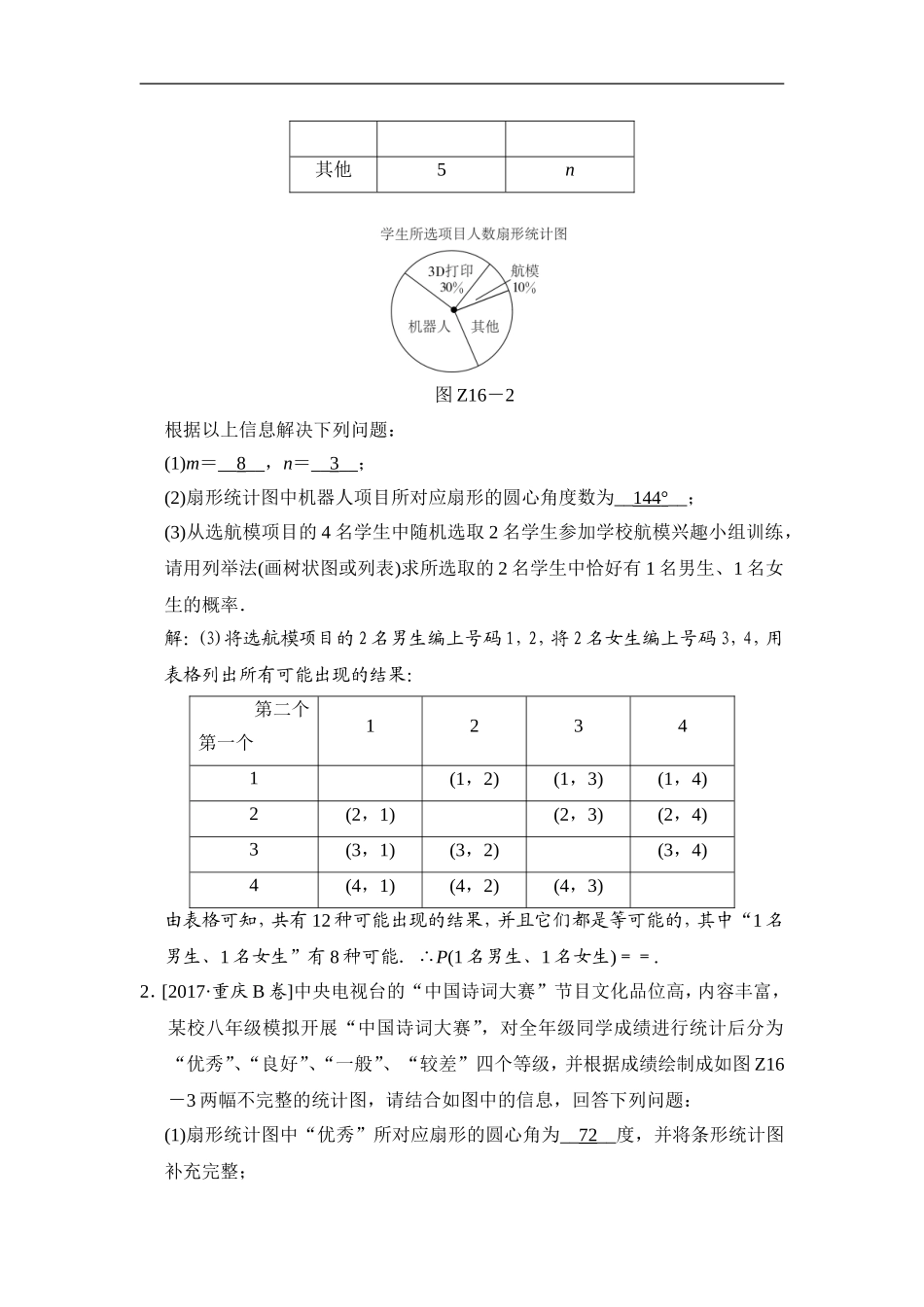
专题提升(十六)统计与概率的综合运用类型之一统计图表在实际生活中的应用【经典母题】如图Z16-1①表示去年某地12个月中每月的平均气温,图②表示该地一家庭在去年12个月的用电量.根据统计图,你能说出该家庭用电量与气温间的关系吗?图Z16-1解:1月份的气温最低,8月份的气温最高;由条形统计图可以看出:1月份和8月份的用电量最多.∴可得到信息:当气温最高或最低时,用电量最多.【点悟】本题考查的是条形统计图和折线统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.【思想方法】能看懂统计图,从统计图中获取信息是中考的基本考题,常见的统计图有条形统计图、扇形统计图、折线统计图和频数分布直方图.要掌握统计图表的优缺点和他们在实际生活中的应用.【中考变形】1.[2017·苏州]七(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果如图Z16-2列出统计表,绘制成扇形统计图.男、女生所选项目人数统计表项目男生(人数)女生(人数)机器人793D打印m4航模22其他5n图Z16-2根据以上信息解决下列问题:(1)m=__8__,n=__3__;(2)扇形统计图中机器人项目所对应扇形的圆心角度数为__144°__;(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.解:(3)将选航模项目的2名男生编上号码1,2,将2名女生编上号码3,4,用表格列出所有可能出现的结果:第二个第一个12341(1,2)(1,3)(1,4)2(2,1)(2,3)(2,4)3(3,1)(3,2)(3,4)4(4,1)(4,2)(4,3)由表格可知,共有12种可能出现的结果,并且它们都是等可能的,其中“1名男生、1名女生”有8种可能.∴P(1名男生、1名女生)==.2.[2017·重庆B卷]中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校八年级模拟开展“中国诗词大赛”,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如图Z16-3两幅不完整的统计图,请结合如图中的信息,回答下列问题:(1)扇形统计图中“优秀”所对应扇形的圆心角为__72__度,并将条形统计图补充完整;(2)此次比赛有四名同学获得满分,分别是甲、乙、丙、丁.现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.图Z16-3解:(1)360...