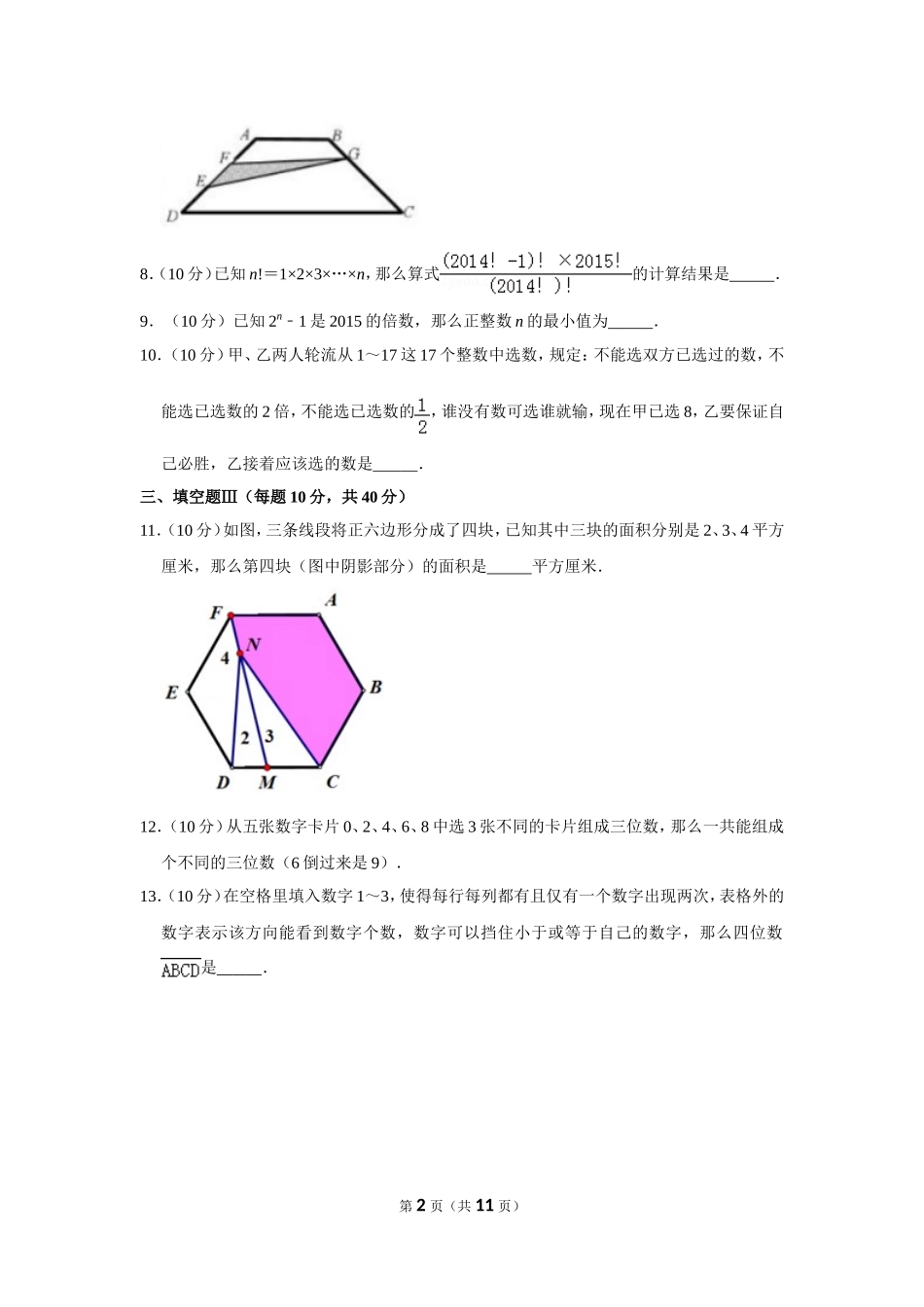
2015年“迎春杯”数学花园探秘科普活动试卷(小高组决赛C卷)一、填空题Ⅰ(每题8分,共32分)1.(6分)算式2015÷(1++++)的计算结果是.2.(6分)如图,在面积为10000平方厘米的长方形中剪去一个大半圆和两个相等的小半圆,那么余下部分(图中阴影)面积是平方厘米.(π取3.14)3.(6分)甲乙两个学徒在讨论谁与师傅一起合作加工一批零件.甲说:“如果我与师傅合作,那么我将完成全部工作的20%.”乙说:“那不算什么,如果我与师傅合作,那么我将完成全部工作的40%.”这时师傅来了,对乙说:“如果甲加入进来帮我们一起做,你就可以少加工60个零件.”如果他们说的话都是正确的,那么这批零件共有个.4.(6分)在每个方框中填入一个数字,使得乘法竖式成立,那么这个算式的乘积是.5.(6分)12个出题老师对本题答案进行猜测,猜测分别为“不小于1”、“不大于2”、“不小于3”、“不大于4”„„“不小于11”、“不大于12”(“不小于”后面是奇数,“不大于”后面是偶数),那么猜对答案的老师人数是人.二、填空题Ⅱ(每题10分,共40分)6.(10分)甲、乙二人合作一项工程,若干天可以完成.若甲单独完成工程的一半,则比甲、乙二人合作完成全部工程提前10天;若乙单独完成工程的一半,则比甲、乙二人合作完成全部工程多用15天,那么甲、乙二人合作完成全部工程需要用天.7.(10分)如图,等腰梯形ABCD中,上底AB为4厘米,下底CD是12厘米,腰AD与下底DC的夹角是45°,如果AF=FE=ED且BC=4BG,那么△EFG的面积是平方厘米.第1页(共11页)8.(10分)已知n!=1×2×3×…×n,那么算式的计算结果是.9.(10分)已知2n﹣1是2015的倍数,那么正整数n的最小值为.10.(10分)甲、乙两人轮流从1~17这17个整数中选数,规定:不能选双方已选过的数,不能选已选数的2倍,不能选已选数的,谁没有数可选谁就输,现在甲已选8,乙要保证自己必胜,乙接着应该选的数是.三、填空题Ⅲ(每题10分,共40分)11.(10分)如图,三条线段将正六边形分成了四块,已知其中三块的面积分别是2、3、4平方厘米,那么第四块(图中阴影部分)的面积是平方厘米.12.(10分)从五张数字卡片0、2、4、6、8中选3张不同的卡片组成三位数,那么一共能组成个不同的三位数(6倒过来是9).13.(10分)在空格里填入数字1~3,使得每行每列都有且仅有一个数字出现两次,表格外的数字表示该方向能看到数字个数,数字可以挡住小于或等于自己的数字,那么四位数是....