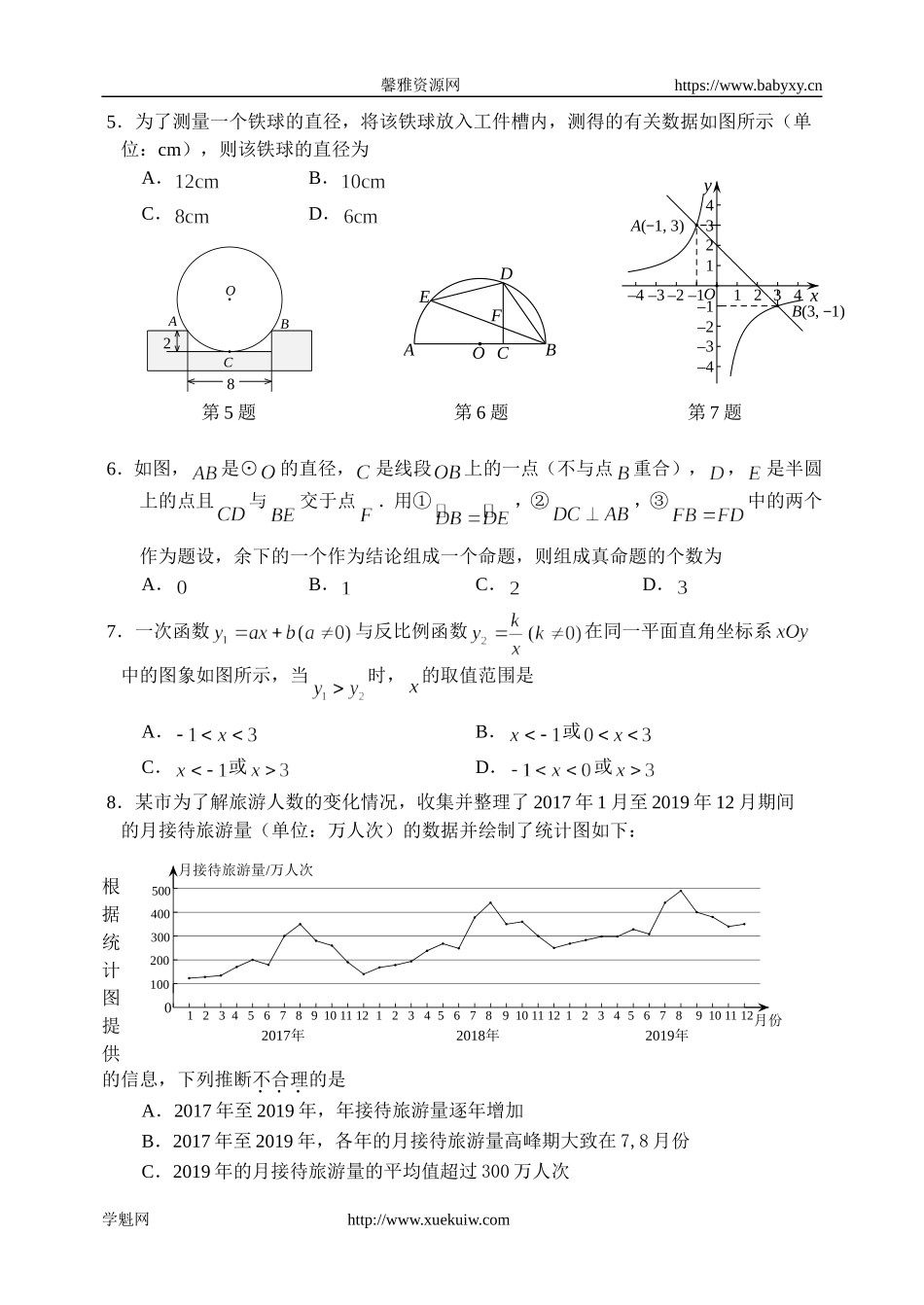
馨雅资源网https://www.babyxy.cn石景山区2019—2020学年第一学期初三期末试卷数学学校姓名准考证号考生须知1.本试卷共8页,共三道大题,28道小题.满分100分,考试时间120分钟.2.在试卷和答题卡上准确填写学校名称、姓名和准考证号.3.试卷答案一律填涂或书写在答题卡上,在试卷上作答无效.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答.4.考试结束,将本试卷和答题卡一并交回.一、选择题(本题共16分,每小题2分)下面各题均有四个选项,符合题意的选项只有一个.1.如图,的顶点都在正方形网格的格点上,则的值为A.B.C.D.2.如图,是⊙的直径,是弦,若,则的度数为A.B.C.D.3.如图,某斜坡的长为,坡顶离水平地面的距离为,则这个斜坡的坡度为A.B.C.D.4.已知抛物线上部分点的横坐标与纵坐标的对应值如下表:…………下列结论:①抛物线开口向下;②当时,随的增大而减小;③抛物线的对称轴是直线;④函数的最大值为2.其中所有正确的结论为A.①②③B.①③C.①③④D.①②③④学魁网http://www.xuekuiw.comDCBAO50m100m第1题第2题第3题ABC馨雅资源网https://www.babyxy.cn5.为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为A.B.C.D.6.如图,是⊙的直径,是线段上的一点(不与点重合),,是半圆上的点且与交于点.用①,②,③中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为A.B.C.D.7.一次函数与反比例函数在同一平面直角坐标系中的图象如图所示,当时,的取值范围是A.B.或C.或D.或8.某市为了解旅游人数的变化情况,收集并整理了2017年1月至2019年12月期间的月接待旅游量(单位:万人次)的数据并绘制了统计图如下:根据统计图提供的信息,下列推断不合理的是A.2017年至2019年,年接待旅游量逐年增加B.2017年至2019年,各年的月接待旅游量高峰期大致在7,8月份C.2019年的月接待旅游量的平均值超过300万人次学魁网http://www.xuekuiw.com5678910111256789101112910111256780月份月接待旅游量/万人次5004003002001002019年2018年2017年123412341234OABC82第5题第6题第7题FEOABCDxyB(3,1)A(1,3)–1–2–3–41234–1–2–3–41234O馨雅资源网https://www.babyxy.cnD.2017年至2019年,各年下半年(7月至12月)的月接待旅游量相对于上半年(1月至6月)波动性更小,变化比较平稳二、填空题(本题...