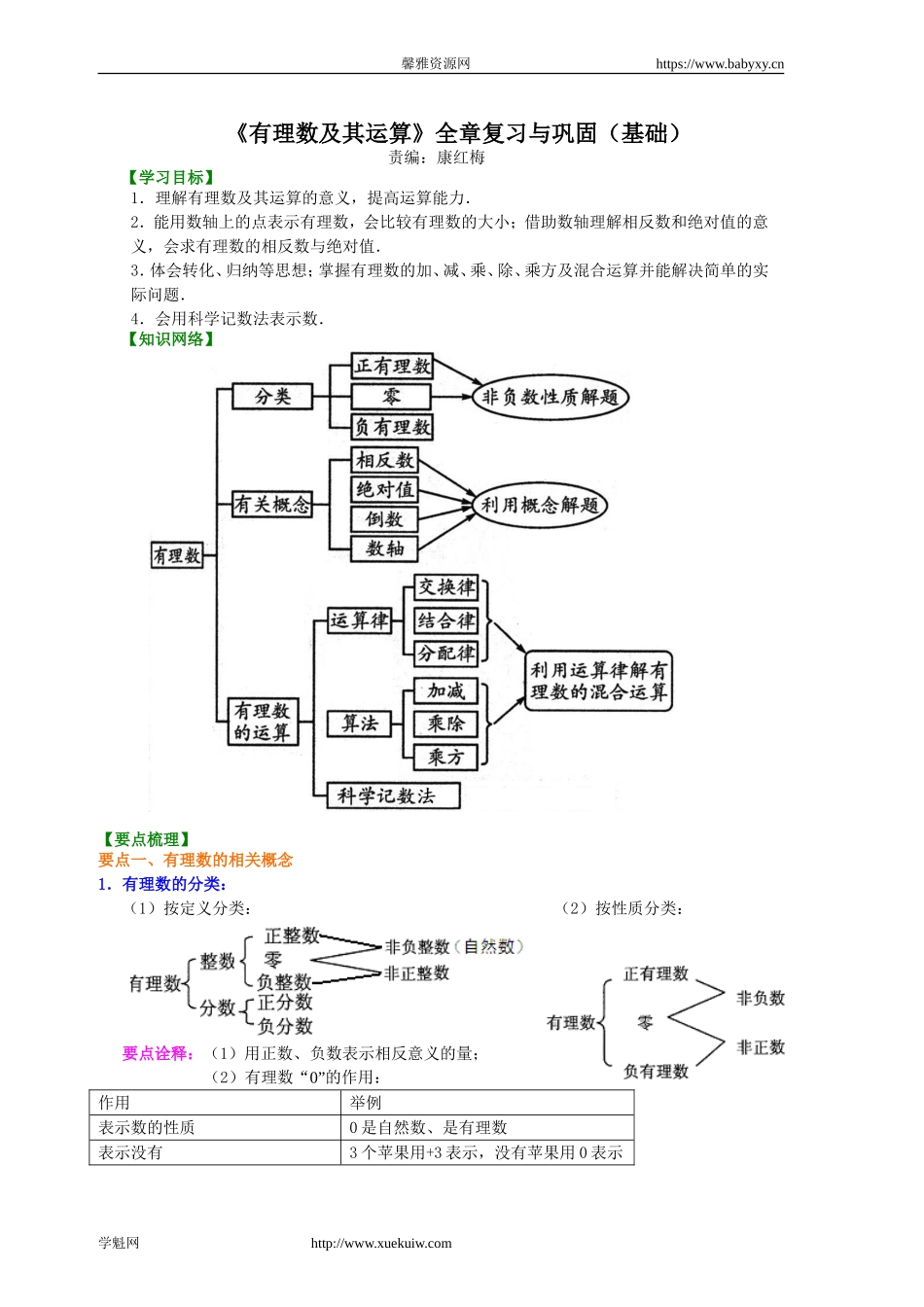
馨雅资源网https://www.babyxy.cn《有理数及其运算》全章复习与巩固(基础)责编:康红梅【学习目标】1.理解有理数及其运算的意义,提高运算能力.2.能用数轴上的点表示有理数,会比较有理数的大小;借助数轴理解相反数和绝对值的意义,会求有理数的相反数与绝对值.3.体会转化、归纳等思想;掌握有理数的加、减、乘、除、乘方及混合运算并能解决简单的实际问题.4.会用科学记数法表示数.【知识网络】【要点梳理】要点一、有理数的相关概念1.有理数的分类:(1)按定义分类:(2)按性质分类:要点诠释:(1)用正数、负数表示相反意义的量;(2)有理数“0”的作用:作用举例表示数的性质0是自然数、是有理数表示没有3个苹果用+3表示,没有苹果用0表示学魁网http://www.xuekuiw.com馨雅资源网https://www.babyxy.cn表示某种状态表示冰点表示正数与负数的界点0非正非负,是一个中性数2.数轴:规定了原点、正方向和单位长度的直线.要点诠释:(1)一切有理数都可以用数轴上的点表示出来,数轴上的点不都表示的是有理数,如.(2)在数轴上,右边的点所对应的数总比左边的点所对应的数大.3.相反数:只有符号不同的两个数互称为相反数,0的相反数是0.要点诠释:(1)一对相反数在数轴上对应的点位于原点两侧,并且到原点的距离相等,这两点是关于原点对称的.(2)求任意一个数的相反数,只要在这个数的前面添上“”号即可.(3)多重符号的化简:数字前面“”号的个数若有偶数个时,化简结果为正,若有奇数个时,化简结果为负.4.绝对值:(1)代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.数a的绝对值记作.(2)几何意义:一个数a的绝对值就是数轴上表示数a的点与原点的距离.要点二、有理数的运算1.法则:(1)加法法则:①同号两数相加,取相同的符号,并把绝对值相加.②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.③一个数同0相加,仍得这个数.(2)减法法则:减去一个数,等于加这个数的相反数.即a-b=a+(-b).(3)乘法法则:①两数相乘,同号得正,异号得负,并把绝对值相乘.②任何数同0相乘,都得0.(4)除法法则:除以一个不等于0的数,等于乘这个数的倒数.即a÷b=a·(b≠0).(5)乘方运算的符号法则:①负数的奇次幂是负数,负数的偶次幂是正数;②正数的任何次幂都是正数,0的任何非零次幂都是0.(6)有理数的混合运算顺序:①先...