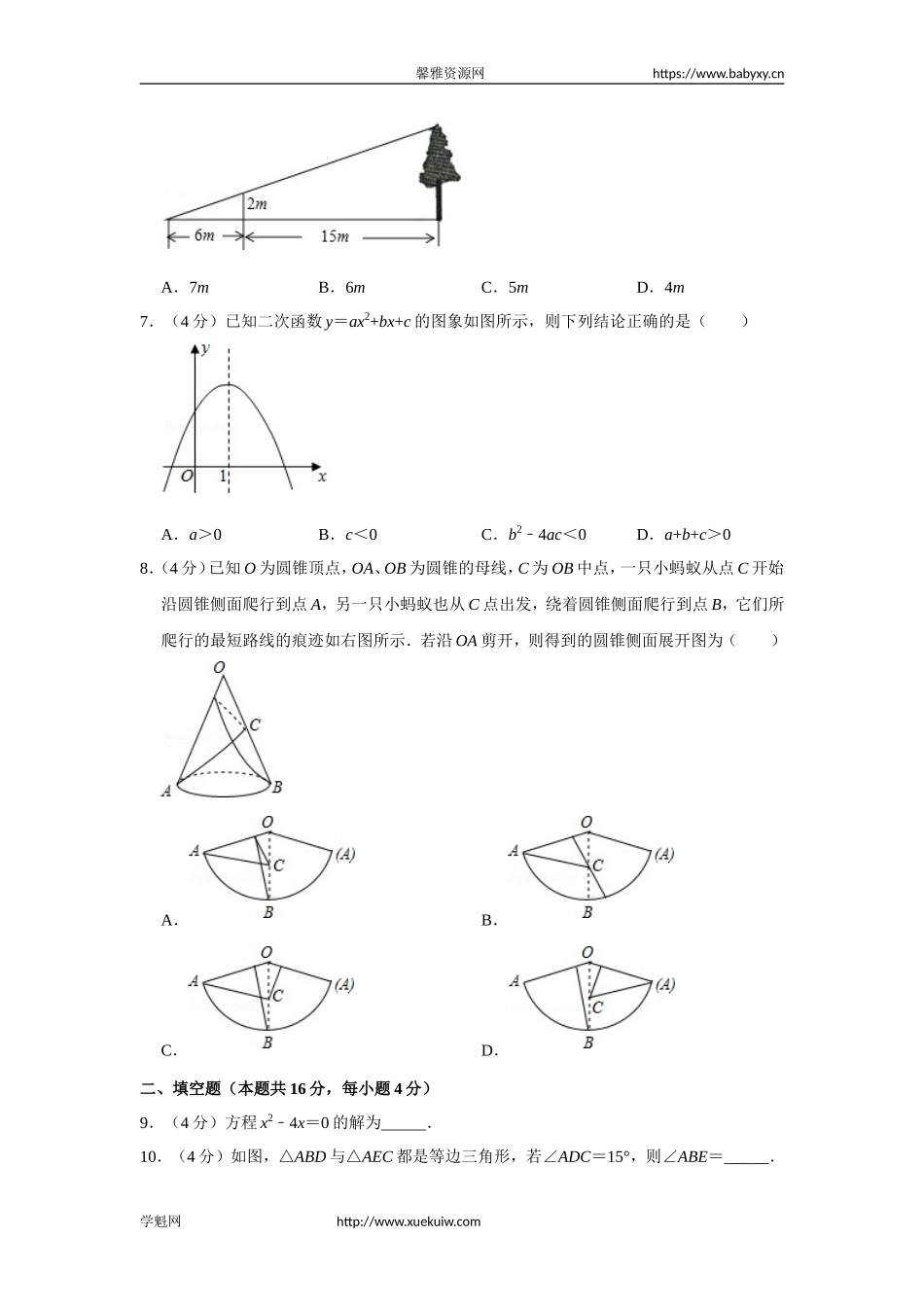
馨雅资源网https://www.babyxy.cn2011-2012学年北京市海淀区九年级(上)期末数学试卷一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的.1.(4分)下列说法正确的是()A.掷两枚硬币,一枚正面朝上,一枚反面超上是不可能事件B.随意地翻到一本书的某页,这页的页码为奇数是随机事件C.经过某市一装有交通信号灯的路口,遇到红灯是必然事件D.某一抽奖活动中奖的概率为买100张奖券一定会中奖2.(4分)下列图形,既是轴对称图形,又是中心对称图形的是()A.B.C.D.3.(4分)将抛物线y=x2平移得到抛物线y=x2+3,则下列平移过程正确的是()A.向上平移3个单位B.向下平移3个单位C.向左平移3个单位D.向右平移3个单位4.(4分)下列一元二次方程有两个相等实数根的是()A.x2﹣x+1=0B.2x2﹣3x﹣1=0C.x2﹣6x+9=0D.x2﹣4x+2=05.(4分)已知圆锥的底面半径为2cm,母线长为5cm,则圆锥的侧面积是()A.20cm2B.20πcm2C.10πcm2D.5πcm26.(4分)如图,为了测量某棵树的高度,小明用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m,与树相距15m,则树的高度是()学魁网http://www.xuekuiw.com馨雅资源网https://www.babyxy.cnA.7mB.6mC.5mD.4m7.(4分)已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是()A.a>0B.c<0C.b2﹣4ac<0D.a+b+c>08.(4分)已知O为圆锥顶点,OA、OB为圆锥的母线,C为OB中点,一只小蚂蚁从点C开始沿圆锥侧面爬行到点A,另一只小蚂蚁也从C点出发,绕着圆锥侧面爬行到点B,它们所爬行的最短路线的痕迹如右图所示.若沿OA剪开,则得到的圆锥侧面展开图为()A.B.C.D.二、填空题(本题共16分,每小题4分)9.(4分)方程x2﹣4x=0的解为.10.(4分)如图,△ABD与△AEC都是等边三角形,若∠ADC=15°,则∠ABE=.学魁网http://www.xuekuiw.com馨雅资源网https://www.babyxy.cn11.(4分)若(x,y,z均不为0),则的值为.12.(4分)用两个全等的含30°角的直角三角形制作如图1所示的两种卡片,两种卡片中扇形的半径均为1,且扇形所在圆的圆心分别为长直角边的中点和30°角的顶点,按先A后B的顺序交替摆放A、B两种卡片得到图2所示的图案.若摆放这个图案共用两种卡片8张,则这个图案中阴影部分的面积之和为;若摆放这个图案共用两种卡片(2n+1)张(n为正整数),则这个...