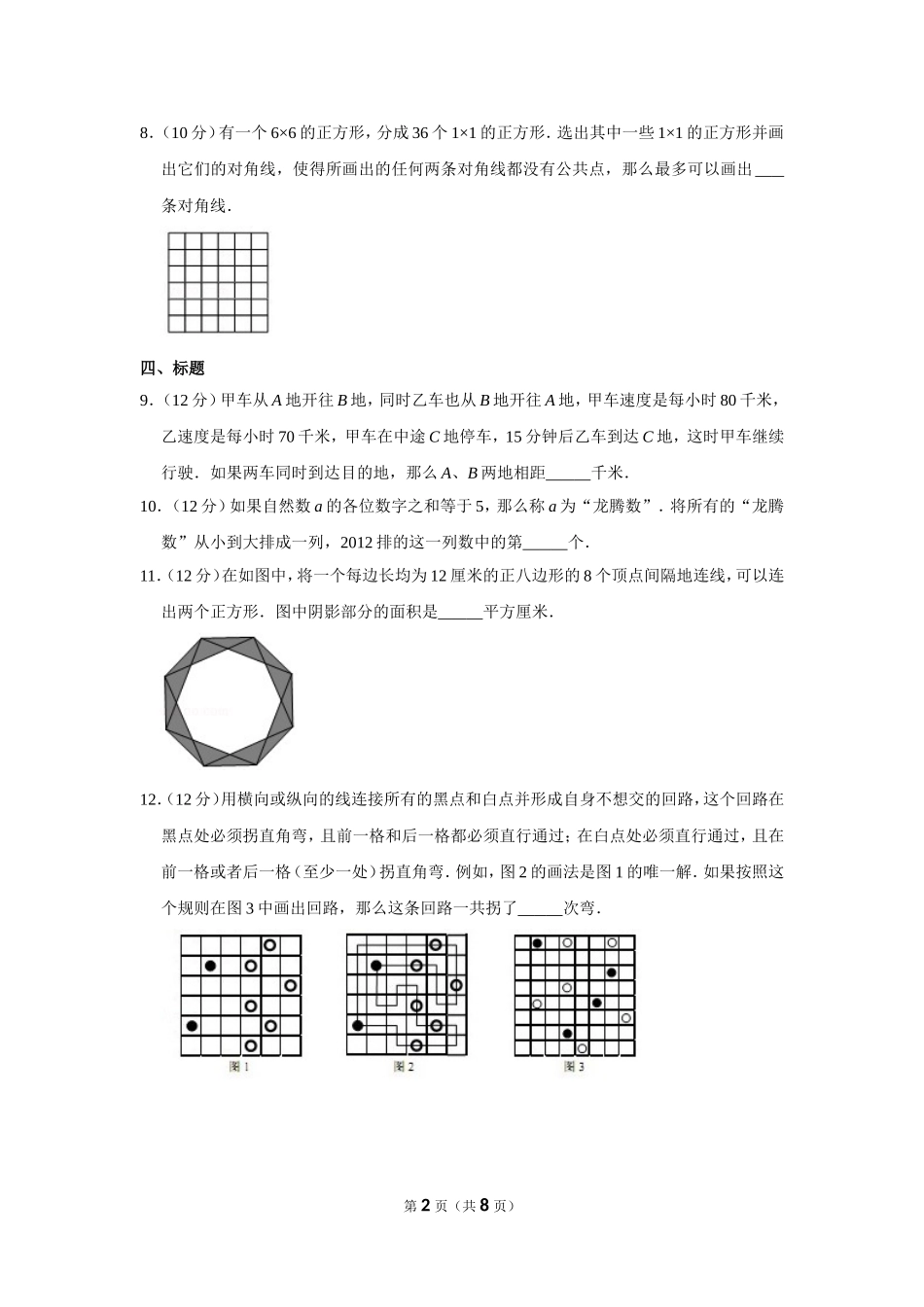
2012年“迎春杯”数学解题能力展示初赛试卷(六年级)一、填空题(每题8分,共32分)1.(8分)算式(9+7+5+3+1)×12的计算结果是.2.(8分)将棱长为5的大正方体切割成125个棱长为1的小正方体,这些小正方体的表面积总和是原大正方体表面积的倍.3.(8分)一辆玩具汽车,第一天按100%的利润定价,无人来买;第二天降价10%,还是无人买;第三天再降价360元,终于卖出.已知卖出的价格是进价的1.44倍,那么这辆玩具汽车的进价是元.4.(8分)在如图中竖式除法中,被除数为.二、填空题(每小题10分,共40分)5.(10分)一个电子钟表上总把日期显示为八位数,如2011年1月1日显示为20110101,那么2011年最后一个能被101整除的日子是,那么=.6.(10分)一个n位正整数x,如果把它补在任意两个正整数的后面,所得两个新数的乘积的末尾还是x,那么称x是“吉祥数”.例如:6就是一个“吉祥数”;但16不是,因为116×216=25056,末尾不再是16.所有位数不超过3位的“吉祥数”之和是.7.(10分)有一个足够深的水槽,底面的长为16厘米、宽为12厘米的长方形,原本在水槽里盛有6厘米深的水和6厘米深的油(油在水的上方).如果在水槽中放入一个长、宽、高分别为8厘米、8厘米、12厘米的铁块,那么油层的层高是厘米.第1页(共8页)8.(10分)有一个6×6的正方形,分成36个1×1的正方形.选出其中一些1×1的正方形并画出它们的对角线,使得所画出的任何两条对角线都没有公共点,那么最多可以画出条对角线.四、标题9.(12分)甲车从A地开往B地,同时乙车也从B地开往A地,甲车速度是每小时80千米,乙速度是每小时70千米,甲车在中途C地停车,15分钟后乙车到达C地,这时甲车继续行驶.如果两车同时到达目的地,那么A、B两地相距千米.10.(12分)如果自然数a的各位数字之和等于5,那么称a为“龙腾数”.将所有的“龙腾数”从小到大排成一列,2012排的这一列数中的第个.11.(12分)在如图中,将一个每边长均为12厘米的正八边形的8个顶点间隔地连线,可以连出两个正方形.图中阴影部分的面积是平方厘米.12.(12分)用横向或纵向的线连接所有的黑点和白点并形成自身不想交的回路,这个回路在黑点处必须拐直角弯,且前一格和后一格都必须直行通过;在白点处必须直行通过,且在前一格或者后一格(至少一处)拐直角弯.例如,图2的画法是图1的唯一解.如果按照这个规则在图3中画出回路,那么这条回路一共拐了次弯.第2页(共8页)2012年“迎春杯”数学解...