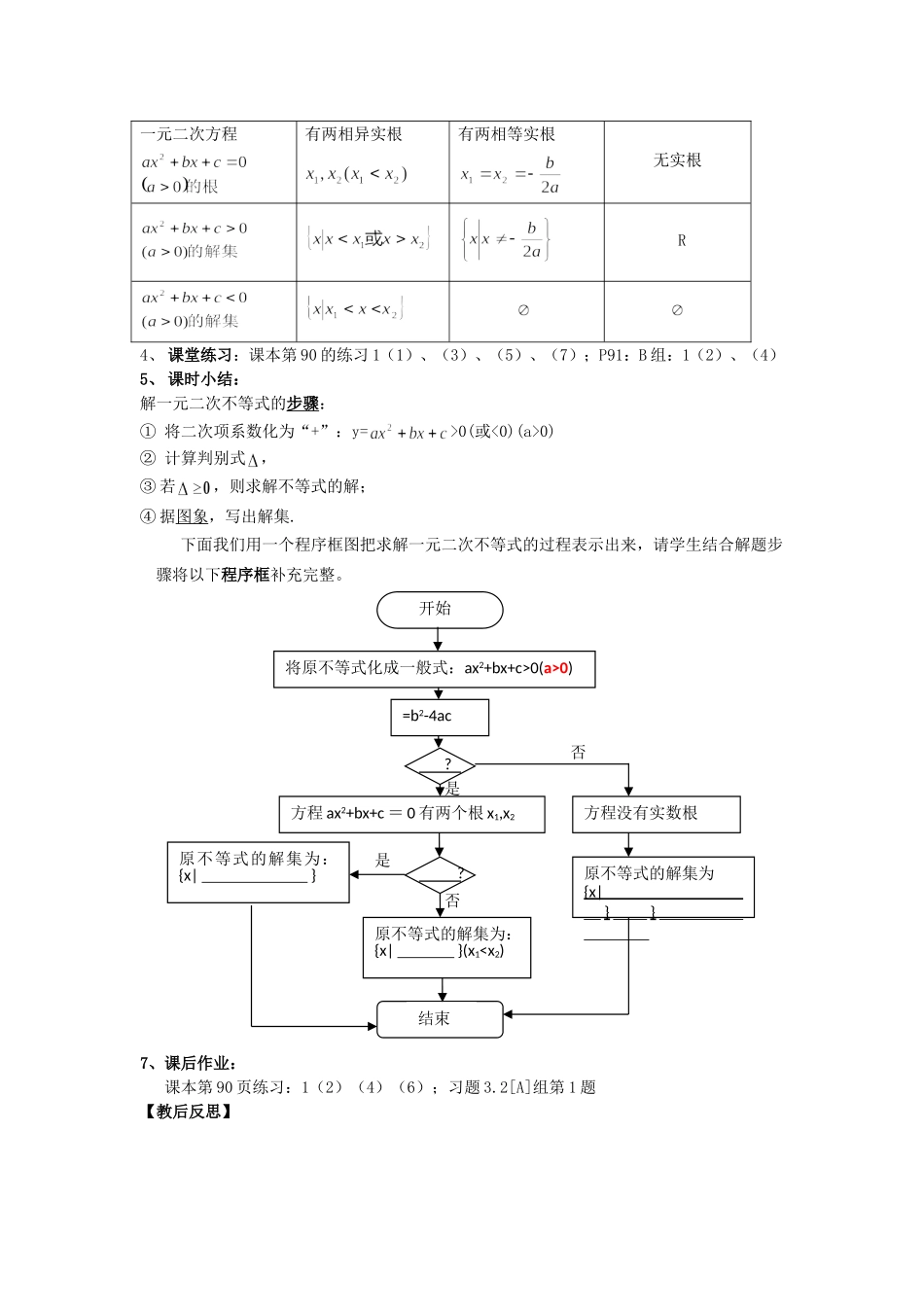
一元二次不等式及其解法(1)三维目标:一、知识与技能1、经历从实际情景中抽象出一元二次不等式模型的过程;2、通过函数图象了解一元二次不等式与二次函数、一元二次方程的联系(即“三个二”);3、会求解一元二次不等式,并从解法中归纳设计求解的程序框图。二、过程与方法1、采用探究法,按照思考、交流、实验、观察、分析、得出结论的方法进行启发式教学;2、通过师的引导,充分发挥学生的主体作用,作好探究性实验;3、理论联系实际,激发学生的学习积极性。三、情感态度与价值观1、通过利用二次函数的图象来求解一元二次不等式的解集,培养学生的数形结合的数学思想;2、通过研究函数、方程与不等式间的内在联系,使学生从中认识到事物间是相互联系、相互转化,密不可分的观点。教学重点:1、从实际问题中抽象出一元二次不等式的模型;2、围绕一元二次不等式的解法展开探究,熟练掌握数形结合的思想与方法。教学难点:“三个二次”间的相互转化的能力培养。教具准备:多媒体及课件、三角板。教学过程:一、创设问题情境,导入新课(投影问题)教材P85互联网的收费问题从实际情境中抽象出一元二次不等式模型:教师引导学生分析问题、解决问题,最后得到一元二次不等式模型:…………………………(1)二、新授课1、一元二次不等式的定义形如,只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式2、探究一元二次不等式的解集问题:怎样求不等式(1)的解集呢?引导学生回顾以前过的一元一次不等式与一元一次方程、一次函数的关系。进而探究:一元二次不等式与一元二次方程、二次函数间又有类似的关系?方程的根与函数的零点:方程有实数根函数的图象与轴有交点函数有零点(1)二次方程的根与二次函数的零点的关系易知:二次方程的有两个实数根:二次函数有两个零点:于是,我们得到:二次方程的根就是二次函数的零点。(2)观察图象,获得解集画出二次函数的图象,如图,观察函数图象,可知:当x<0,或x>5时,函数图象位于x轴上方,此时,y>0,即;当00解:因为(2)x2-2x+3<0解:因为无实数解,所以不等式的解集是.变式:若求不等式-2x2+3x+2<0的解集?(培养学生转化化归的思想)4、探究一般的一元二次不等式的解法任意的一元二...