高中数学人教A版选修4-1学业分层测评1 平行线等分线段定理 Word版含解析.doc

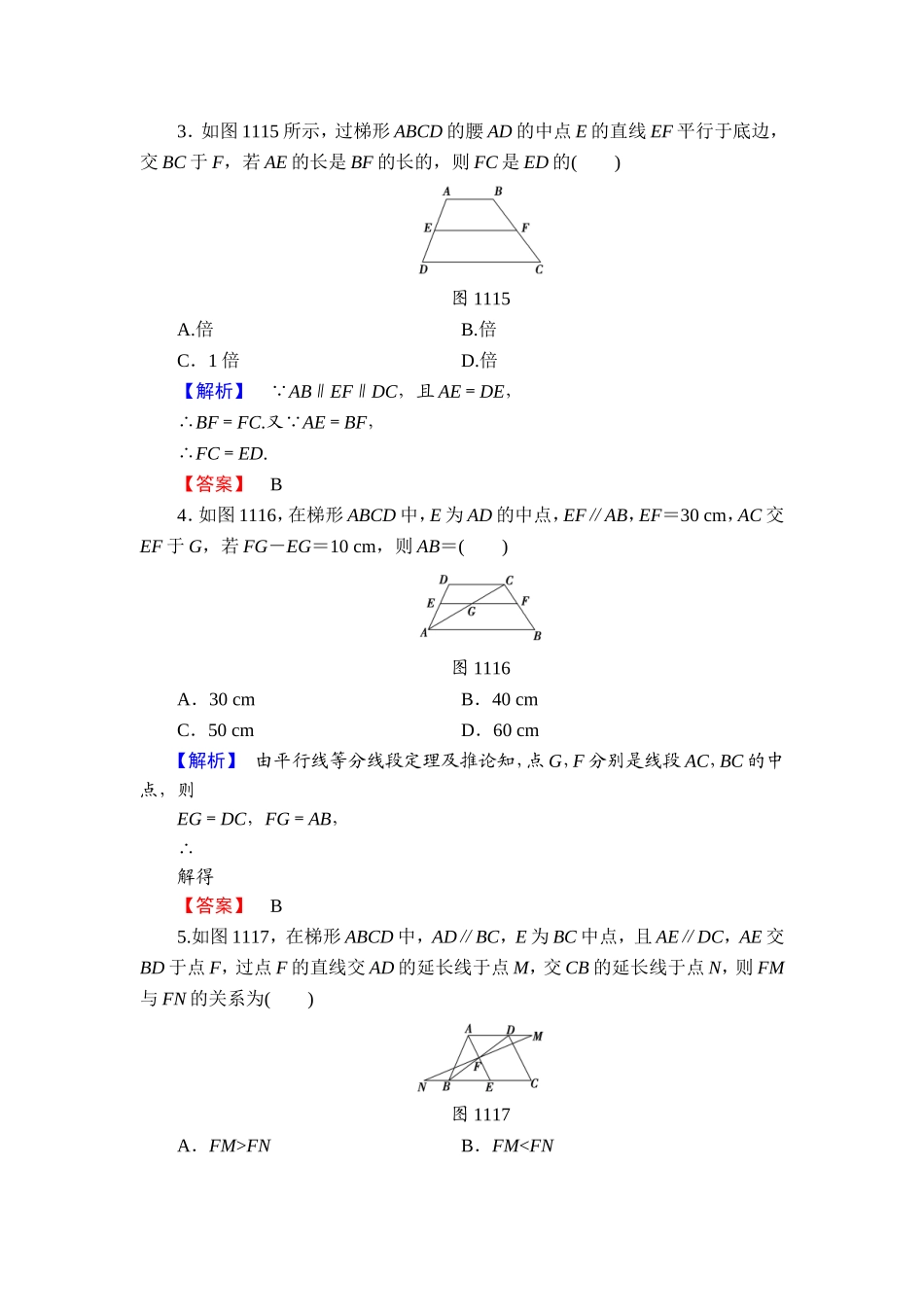
学业分层测评(一) (建议用时：45分钟) [学业达标] 一、选择题 1．如图1­1­13，已知l1∥l2∥l3，AB，CD相交于l2上一点O，且AO＝OB，则下列结论中错误的是(　　) 图1­1­13 A．AC＝BD B．AE＝ED C．OC＝OD D．OD＝OB 【解析】　由l1∥l2∥l3知AE＝ED，OC＝OD， 由△AOC≌△BOD知AC＝BD， 但OD与OB不能确定其大小关系． 故选D. 【答案】　D 2．如图1­1­14，已知AE⊥EC，CE平分∠ACB ，DE∥BC，则DE等于(　　) 【导学号：07370003】 图1­1­14 A．BC－AC B．AC－BF C.(AB－AC) D.(BC－AC) 【解析】　由已知得CE是线段AF的垂直平分线． ∴AC＝FC，AE＝EF. ∵DE∥BC， ∴DE是△ABF的中位线， ∴DE＝BF＝(BC－AC)． 【答案】　D 3．如图1­1­15所示，过梯形ABCD的腰AD的中点E的直线EF平行于底边，交BC于F，若AE的长是BF的长的，则FC是ED的(　　) 图1­1­15 A.倍 B.倍 C．1倍 D.倍 【解析】　∵AB∥EF∥DC，且AE＝DE， ∴BF＝FC.又∵AE＝BF， ∴FC＝ED. 【答案】　B 4．如图1­1­16，在梯形ABCD中，E为AD的中点，EF∥AB，EF＝30 cm，AC交EF于G，若FG－EG＝10 cm，则AB＝(　　) 图1­1­16 A．30 cm B．40 cm C．50 cm D．60 cm 【解析】　由平行线等分线段定理及推论知，点G，F分别是线段AC，BC的中点，则 EG＝DC，FG＝AB， ∴ 解得 【答案】　B 5.如图1­1­17，在梯形ABCD中，AD∥BC，E为BC中点，且AE∥DC，AE交BD于点F，过点F的直线交AD的延长线于点M，交CB的延长线于点N，则FM与FN的关系为(　　) 图1­1­17 A．FM>FN　　 B．FM<FN C．FM＝FN D．不能确定 【解析】　∵AD∥BC，AE∥DC， ∴四边形AECD是平行四边形. ∴AD＝EC＝BC， 即BE＝EC＝AD. ∴△ADF≌△EBF， ∴AF＝FE， ∴△AFM≌△EFN， ∴FM＝FN. 【答案】　C 二、填空题 6．如图1­1­18所示，在梯形ABCD中，AD∥BC，AD＝2，BC＝6，E，F分别为对角线BD，AC的中点，则EF＝____. 图1­1­18 【解析】　如图所示，过E作GE∥BC交BA于G. ∵E是DB的中点， ∴G是AB的中点，又F是AC的中点， ∴GF∥BC，∴G，E，F三点共线， ∴GE＝AD＝1，GF＝BC＝3， ∴EF＝GF－GE＝3－1＝2. 【答案】　2 7．如图1­1­19，已知在△ABC中，AD∶DC＝1∶1，E为BD的中点，AE延长线交BC于F，则BF与FC的比值为__________． 【导学号：07370004】 图1­1­19 【解析】　过D作DG平行于BC，交AF于点G，再根据平行线等分线段定理即可解决． 【答案】　 8．如图1­1­20，在△ABC中，E是AB的中点，EF∥BD，EG∥AC，CD＝AD，若EG＝5 cm，则AC＝________；若BD＝20 cm，则EF＝________. 图1­1­20 【解析】　∵E为AB的中点，EF∥BD， ∴F为AD的中点． ∵E为AB的中点，EG∥AC，∴G为BD的中点，若EG＝5 cm，则AD＝10 cm，又CD＝AD＝5 cm，∴AC＝15 cm.若BD＝20 cm ，则EF＝BD＝10 cm. 【答案】　15 cm　10 cm 三、解答题 9．(2016·南京模拟)如图1­1­21，在梯形ABCD中，CD⊥BC，AD∥BC，E为腰CD的中点，且AD＝2 cm，BC＝8 cm，AB＝10 cm，求BE的长度． 图1­1­21 【解】　过E点作直线EF平行于BC，交AB于F，作BG⊥EF于G(如图)， 因为E为腰CD的中点，所以F为AB的中点，所以BF＝AB＝5 cm， 又EF＝＝＝5(cm)， GF＝BC－FE＝8 cm－5 cm＝3 cm， 所以GB＝＝＝4 cm， EC＝GB＝4 cm， 所以BE＝＝＝4(cm)． 10．用一张矩形纸，你能折出一个等边三角形吗？如图1­1­22(1)，先把矩形纸ABCD对折，设折痕为MN；再把B点叠在折痕线上，得到Rt△ABE，沿着EB线折叠，就能得到等边△EAF，如图(2)．想一想，为什么？ 图1­1­22 【解】　利用平行线等分线段定理的推论2， ∵N是梯形ADCE的腰CD的中点，NP∥AD， ∴P为EA的中点． ∵在Rt△ABE中，PA＝PB(直角三角形斜边上的中线等于斜边的一半)， ∴∠1＝∠3. 又∵PB∥AD， ∴∠3＝∠2，∴∠1＝∠2. 又∵∠1与和它重合的角相等， ∴∠1＝∠2＝30°. 在Rt△AEB中，∠AEB＝60°，∠1＋∠2＝60°， ∴△AEF是等边三角形． [能力提升] 1．如图1­1­23，AD是△ABC的高，E为AB的中点，EF⊥BC于F，如果DC＝BD，那么FC是BF的(　　) 图1­1­23 A.倍　　　　 B.倍 C.倍 D.倍 【解析】　∵EF⊥BC，AD⊥BC，∴EF∥AD. 又E为AB的中点，由推论1知F为BD的中点， 即BF＝FD. 又∵DC＝BD，∴DC＝BF. ∴FC＝FD＋DC＝BF＋DC＝BF. 【答案】　A 2．梯形的一腰长10 cm，该腰和底边所形成的角为30°，中位线长为12 cm，则此梯形的面积为(　　) A．30 cm2 B．40 cm2 C．50 cm2 D．60 cm2 【解析】　如图，过A作AE⊥BC，在Rt△ABE中，AE＝ABsin 30°＝5 cm.又已知梯形的中位线长为12 cm， ∴AD＋BC＝2×12＝24(cm)． ∴梯形的面积S＝(AD＋BC)·AE ＝×5×24＝60(cm2)． 【答案】　D 3．如图1­1­24，AB＝AC，AD⊥BC于D，M是AD的中点，CM交AB于P，DN∥CP，若AB＝9 cm，则AP＝__________；若PM＝1 cm，则PC＝__________. 【导学号：07370005】 图1­1­24 【解析】　由AB＝AC和AD⊥BC，结合等腰三角形的性质，得D是BC的中点．再由DN∥CP，可得N是BP的中点．同理可得P是AN的中点，由此可得答案． 【答案】　3 cm　4 cm 4．如图1­1­25所示，AE∥BF∥CG∥DH，AB＝BC＝CD，AE＝12，DH＝16，AH交BF于点M，求BM与CG的长． 图1­1­25 【解】　如图，取BC的中点P，作PQ∥DH交EH于点Q，则PQ是梯形ADHE的中位线． ∵AE∥BF∥CG∥DH， AB＝BC＝CD， AE＝12，DH＝16， ∴＝，＝， ∴＝， ∴BM＝4. ∵PQ为梯形的中位线， ∴PQ＝(AE＋DH)＝(12＋16)＝14. 同理，CG＝(PQ＋DH)＝(14＋16)＝15.