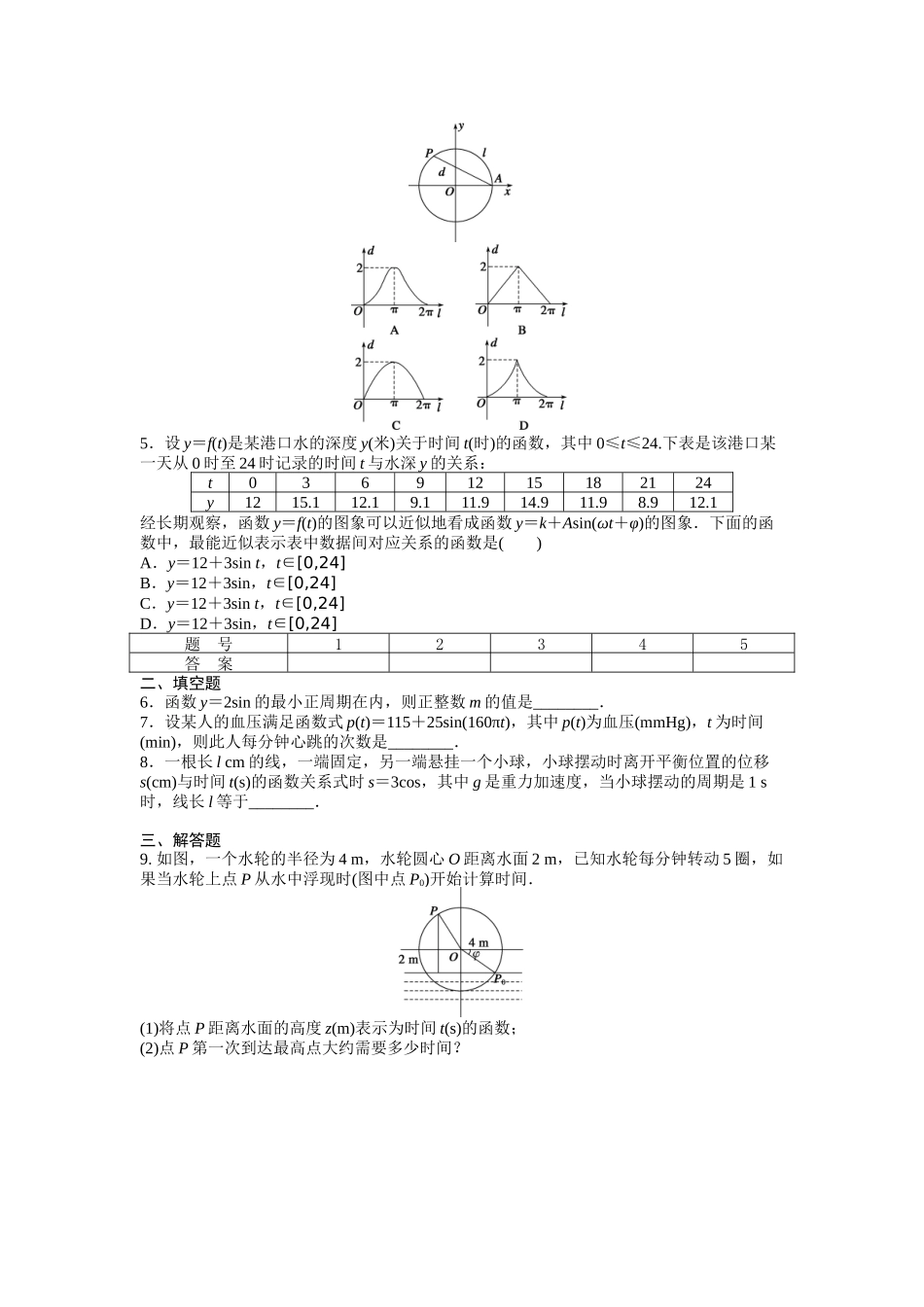
§1.6三角函数模型的简单应用课时目标1.会解三角形和利用三角形建立数学模型,解决实际问题.2.会用三角函数解决一些简单的实际问题,体会三角函数是描述周期变化现象的重要函数模型.1.三角函数的周期性y=Asin(ωx+φ)(ω≠0)的周期是T=________;y=Acos(ωx+φ)(ω≠0)的周期是T=________;y=Atan(ωx+φ)(ω≠0)的周期是T=________.2.函数y=Asin(ωx+φ)+k(A>0,ω>0)的性质(1)ymax=________,ymin=________.(2)A=________________,k=________________________________.(3)ω可由________________确定,其中周期T可观察图象获得.(4)由ωx1+φ=________,ωx2+φ=________,ωx3+φ=______,ωx4+φ=____________,ωx5+φ=________中的一个确定φ的值.3.三角函数模型的应用三角函数作为描述现实世界中________现象的一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测其未来等方面都发挥着十分重要的作用.一、选择题1.如图所示,单摆从某点开始来回摆动,离开平衡位置O的距离scm和时间ts的函数关系式为s=6sin,那么单摆来回摆动一次所需的时间为()A.sB.sC.50sD.100s2.据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈f(x)=Asin(ωx+φ)+b的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定f(x)的解析式为()A.f(x)=2sin+7(1≤x≤12,x∈N*)B.f(x)=9sin(1≤x≤12,x∈N*)C.f(x)=2sinx+7(1≤x≤12,x∈N*)D.f(x)=2sin+7(1≤x≤12,x∈N*)3.若函数f(x)=3sin(ωx+φ)对任意x都有f=f,则f等于()A.3或0B.-3或0C.0D.-3或34.如图所示,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图象大致是()5.设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:t03691215182124y1215.112.19.111.914.911.98.912.1经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是()A.y=12+3sint,t∈[0,24]B.y=12+3sin,t∈[0,24]C.y=12+3sint,t∈[0,24]D.y=12+3sin,t∈[0,24]题号12345答案二、填空题6.函数y=2sin的最小正周期在内,则正整数m的值是________.7.设某人的血压满足函数式p(...