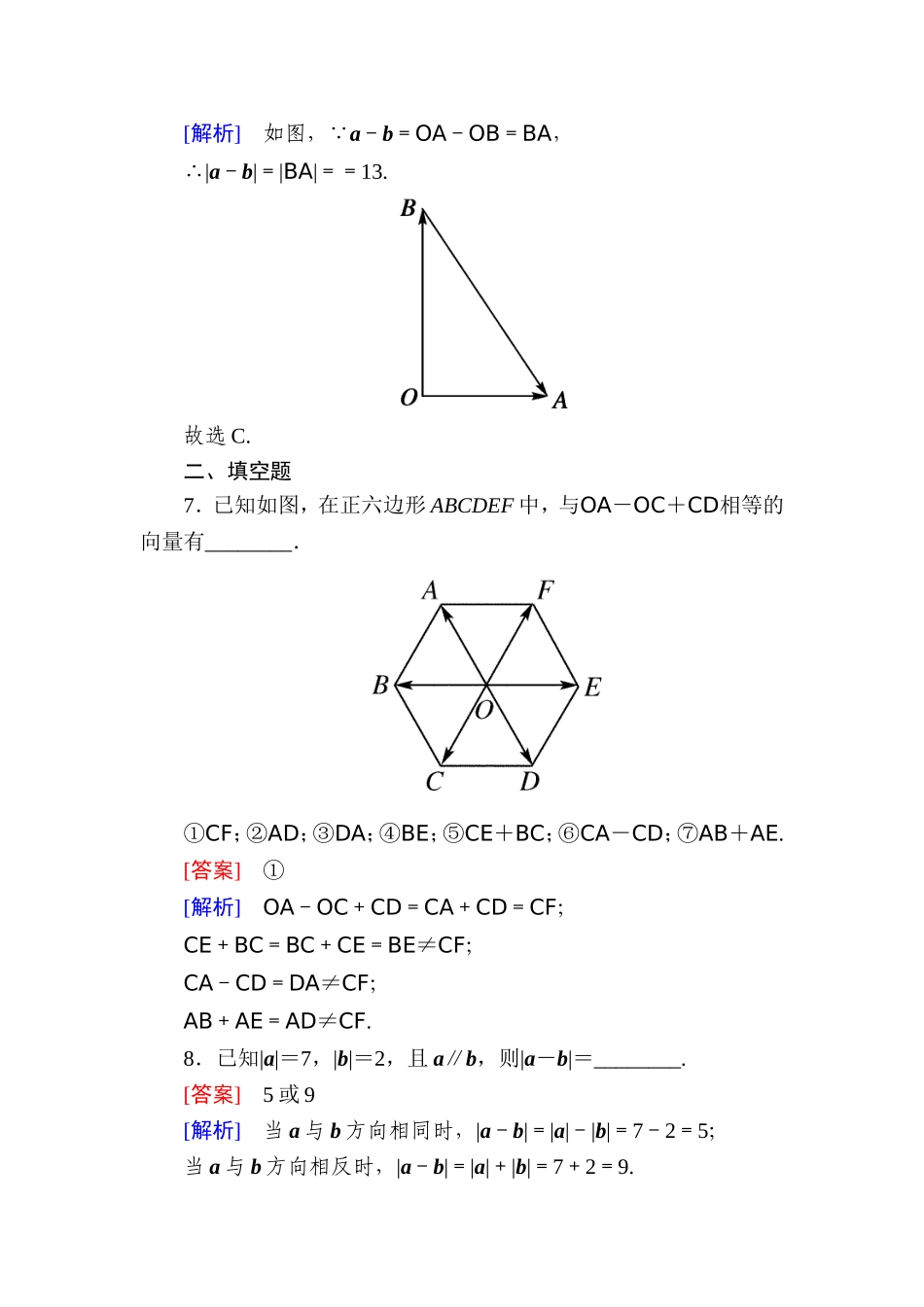
能力提升一、选择题1.化简以下各式:①AB+BC+CA;②AB-AC+BD-CD;③OA-OD+AD;④NQ+QP+MN-MP.结果为零向量的个数是()A.1B.2C.3D.4[答案]D[解析]①AB+BC+CA=AC+CA=AC-AC=0;②AB-AC+BD-CD=(AB+BD)-(AC+CD)=AD-AD=0;③OA-OD+AD=(OA+AD)-OD=OD-OD=0;④NQ+QP+MN-MP=NP+PM+MN=NM-NM=0.2.若|AB|=8,|AC|=5,则|BC|的取值范围是()A.[3,8]B.(3,8)C.[3,13]D.(3,13,)[答案]C[解析]由于BC=AC-AB,则有|AB|-|AC|≤|BC|≤|AB|+|AC|,即3≤|BC|≤13.3.(2011·湖南高考)若O、E、F是不共线的任意三点,则以下各式中成立的是()A.EF=OF+OEB.EF=OF-OEC.EF=-OF+OED.EF=-OF-OE[答案]B[解析]由向量的减法的定义求解.4.已知△ABC的三个顶点A、B、C及平面内一点P满足PA+PB=PC,下列结论中正确的是()A.P在△ABC的内部B.P在△ABC的边AB上C.P在AB边所在直线上D.P在△ABC的外部[答案]D[解析]由PA+PB=PC可得PA=PC-PB=BC,∴四边形PBCA为平行四边形.可知点P在△ABC的外部.选D.5.(四川高考改编)设点M是线段BC的中点,点A在直线BC外,|BC|2=16,|AB+AC|=|AB-AC|,则|AM|=()A.8B.4C.2D.1[答案]C[解析]以AB、AC为邻边作平行四边形ACDB,则由向量加、减法的几何意义可知AD=AB+AC,CB=AB-AC,因为|AB+AC|=|AB-AC|,所以|AD|=|CB|.又四边形ACDB为平行四边形,所以四边形ACDB为矩形,故AC⊥AB.则AM为Rt△ABC斜边BC上的中线,因此,|AM|=|BC|=2.6.已知OA=a,OB=b,|OA|=5,|OB|=12,∠AOB=90°,则|a-b|=________.()A.7B.17C.13D.8[答案]C[解析]如图, a-b=OA-OB=BA,∴|a-b|=|BA|==13.故选C.二、填空题7.已知如图,在正六边形ABCDEF中,与OA-OC+CD相等的向量有________.①CF;②AD;③DA;④BE;⑤CE+BC;⑥CA-CD;⑦AB+AE.[答案]①[解析]OA-OC+CD=CA+CD=CF;CE+BC=BC+CE=BE≠CF;CA-CD=DA≠CF;AB+AE=AD≠CF.8.已知|a|=7,|b|=2,且a∥b,则|a-b|=________.[答案]5或9[解析]当a与b方向相同时,|a-b|=|a|-|b|=7-2=5;当a与b方向相反时,|a-b|=|a|+|b|=7+2=9.9.在△OAB中,已知OA=a,OB=b,且|a|=|b|=4,∠AOB=60°,则|a-b|=________.[答案]4[解析] |a|=|b|,∴OA=OB.又∠AOB=60°,∴△ABO是等边三角形,∴BA=4,∴|a-b|=|OA-OB|=|BA|=4.三、解答题10.在平行四边形ABCD中,AB=a,AD=b,...