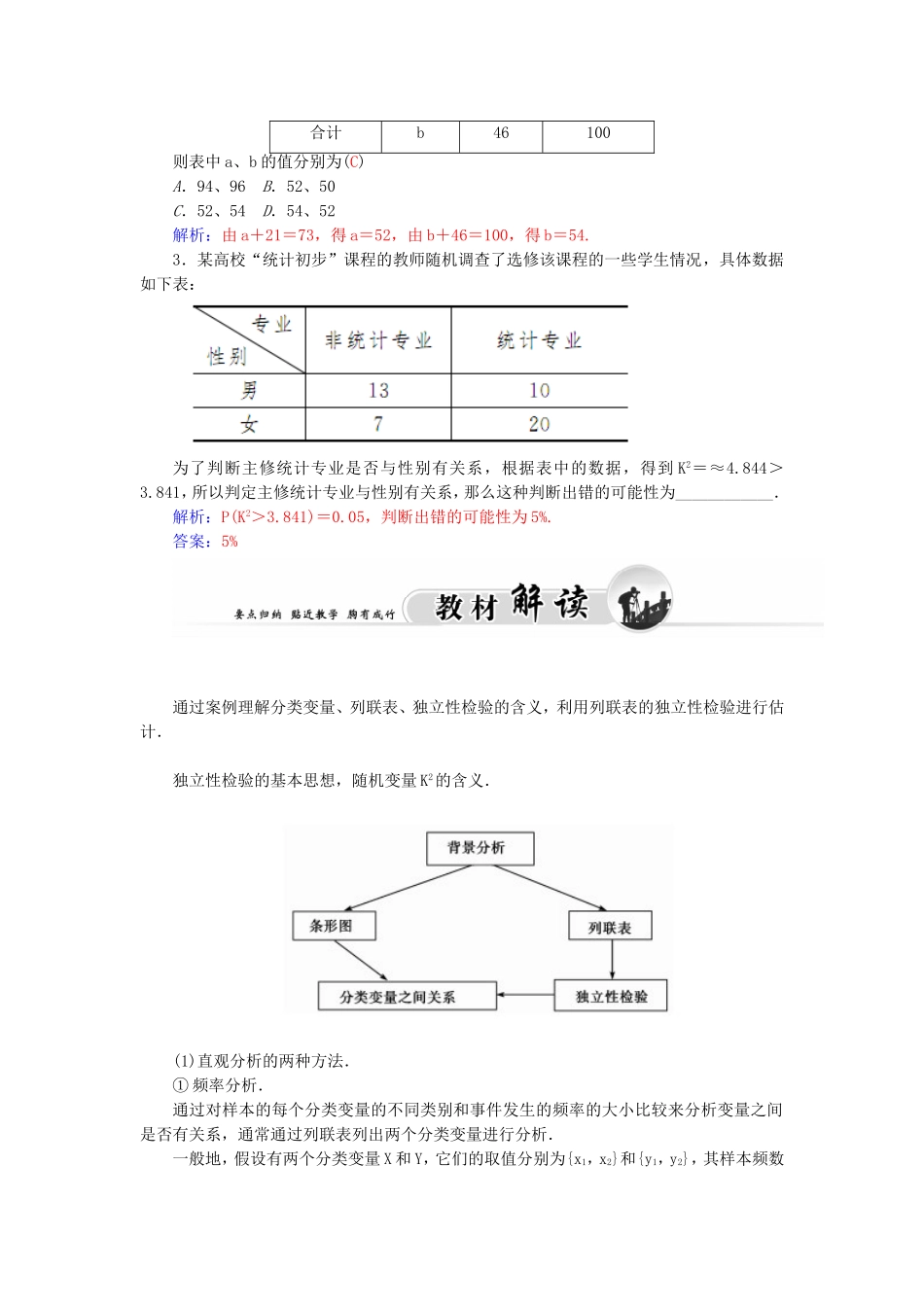
1.2独立性检验的基本思想及其初步应用1.分类变量的定义.如果某种变量的不同“值”表示个体所属的不同类别,像这样的变量称为分类变量.2.2×2列联表.一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:y1y2总计x1aba+bx2cdc+d总计a+cb+da+b+c+d3.独立性检验.,1.下列变量中不属于分类变量的是(B)A.性别B.吸烟C.宗教信仰D.国籍解析:“吸烟”不是分类变量,“是否吸烟”才是分类变量.故选B.2.下面是一个2×2列联表y1y2合计x1a2173x222527合计b46100则表中a、b的值分别为(C)A.94、96B.52、50C.52、54D.54、52解析:由a+21=73,得a=52,由b+46=100,得b=54.3.某高校“统计初步”课程的教师随机调查了选修该课程的一些学生情况,具体数据如下表:为了判断主修统计专业是否与性别有关系,根据表中的数据,得到K2=≈4.844>3.841,所以判定主修统计专业与性别有关系,那么这种判断出错的可能性为____________.解析:P(K2>3.841)=0.05,判断出错的可能性为5%.答案:5%通过案例理解分类变量、列联表、独立性检验的含义,利用列联表的独立性检验进行估计.独立性检验的基本思想,随机变量K2的含义.(1)直观分析的两种方法.①频率分析.通过对样本的每个分类变量的不同类别和事件发生的频率的大小比较来分析变量之间是否有关系,通常通过列联表列出两个分类变量进行分析.一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:yxy1y2总计x1aba+bx2cdc+d总计a+cb+da+b+c+d在列联表中,如果两个分类变量没有关系,则应该满足ad-bc≈0.因此|ad-bc|越小,说明两个分量之间的关系越弱;|ad-bc|越大,说明两个分类变量之间的关系越强.②图形分析.利用等高条形图来分析两分类变量之间是否具有相关关系,形象、直观地反映两个分类变量之间的总体状态和差异大小,进而推断它们之间是否有关系.a.绘制等高条形图时,列联表的行对应的是高度,两行的数据不相等,但对应的条形图的高度是相同的,两列的数据对应不同颜色.b.等高条形图中有两个高度相同的矩形,每一个矩形中都有两种颜色,观察下方颜色区域的高度,如果两个高度相差比较明显,就判断两个分类变量之间有关系.(2)独立性检验及其基本思想.①独立性检验.利用随机变量K2来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类...