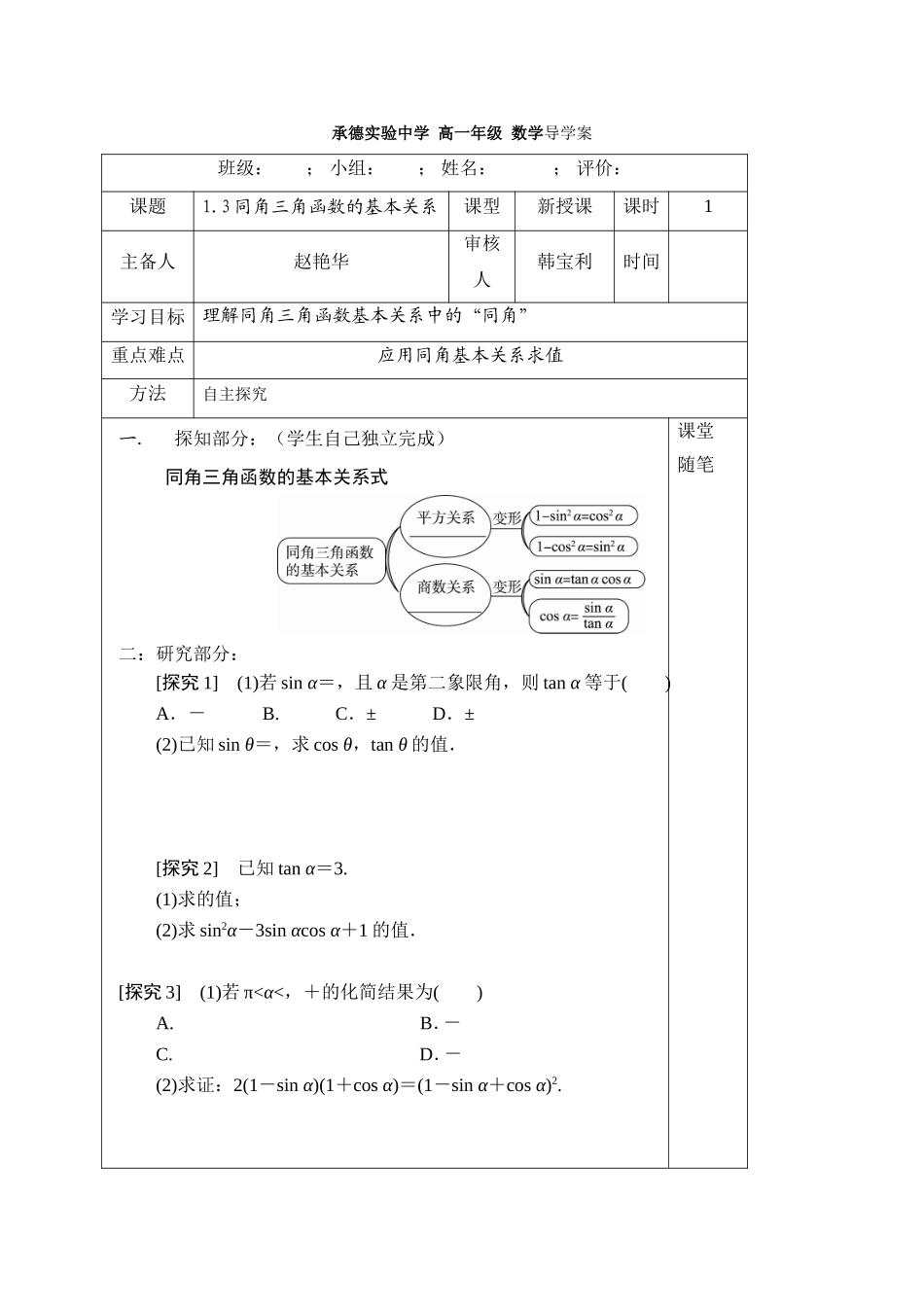
承德实验中学高一年级数学导学案班级:;小组:;姓名:;评价:课题1.3同角三角函数的基本关系课型新授课课时1主备人赵艳华审核人韩宝利时间学习目标理解同角三角函数基本关系中的“同角”重点难点应用同角基本关系求值方法自主探究一.探知部分:(学生自己独立完成)同角三角函数的基本关系式二:研究部分:[探究1](1)若sinα=,且α是第二象限角,则tanα等于()A.-B.C.±D.±(2)已知sinθ=,求cosθ,tanθ的值.[探究2]已知tanα=3.(1)求的值;(2)求sin2α-3sinαcosα+1的值.[探究3](1)若π<α<,+的化简结果为()A.B.-C.D.-(2)求证:2(1-sinα)(1+cosα)=(1-sinα+cosα)2.课堂随笔三:应用部分:1.已知α是第二象限角,sinα=,则cosα=()A.-B.-C.D.2.已知tanα=,α是第三象限角,求sinα,cosα的值.3已知tanα=3,则2sin2α+4sinα·cosα-9cos2α的值为()A.3B.C.D.41.若α为第二象限角,则=()A.sinαB.-sinαC.cosαD.-cosα2.证明下列三角恒等式:(1)=;(2)=.四:巩固部分:1.函数y=+的值域是()A.{0,2}B.{-2,0}C.{-2,0,2}D.{-2,2}2.已知α是第四象限角,tanα=-,则sinα=()A.B.-C.D.-3.已知2cos2α+3cosαsinα-3sin2α=1,求:(1)tanα;(2).4.求证:=.