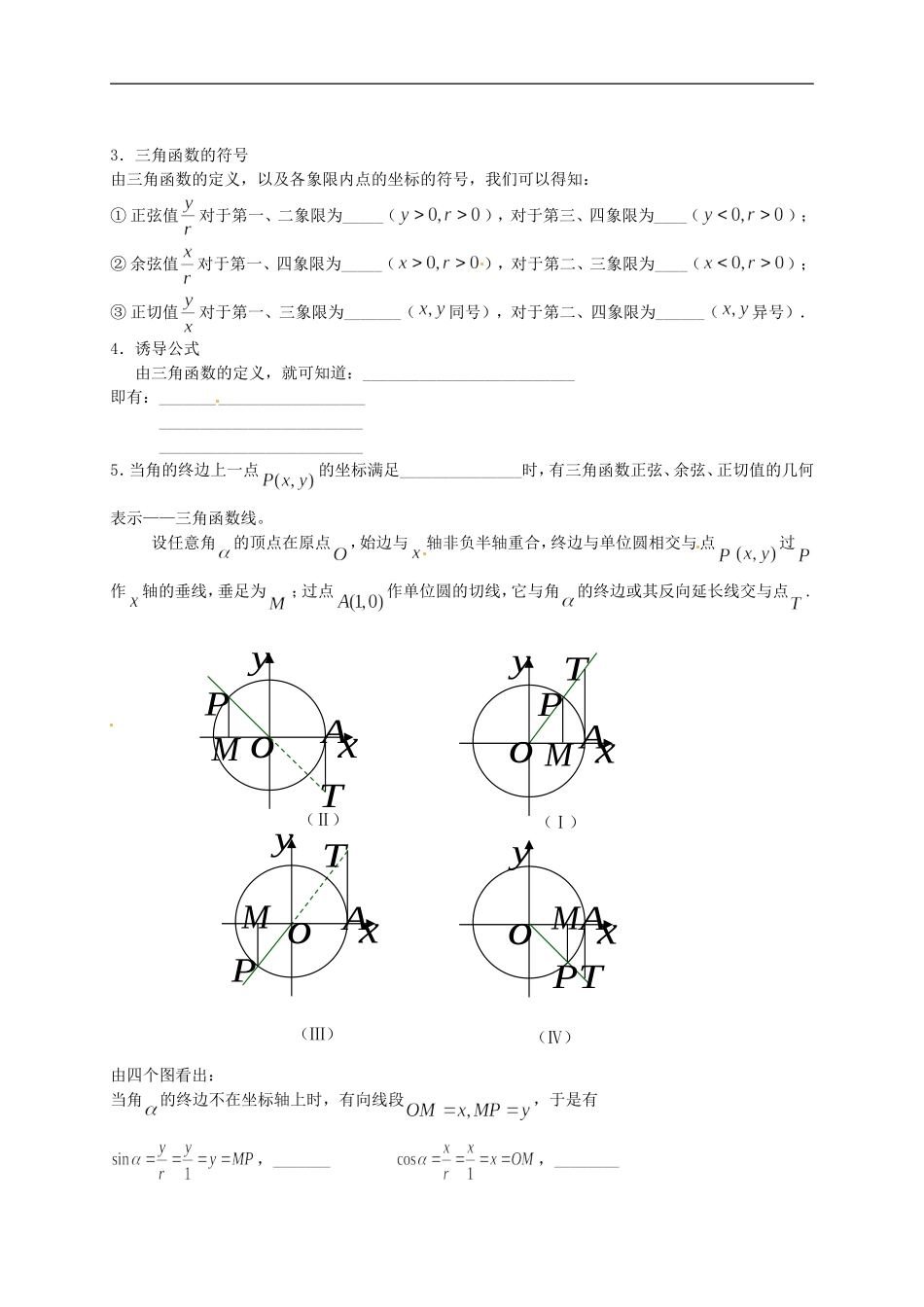
1.21《任意角的三角函数》导学案【学习目标】(1)掌握任意角的正弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号)[来源:Z+xx+k.Com](2)理解任意角的三角函数不同的定义方法;(3)了解如何利用与单位圆有关的有向线段,将任意角α的正弦、余弦、正切函数值分别用正弦线、余弦线、正切线表示出来;(4)掌握并能初步运用公式一;(5)树立映射观点,正确理解三角函数是以实数为自变量的函数.【重点难点】重点:任意角的正弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号);终边相同的角的同一三角函数值相等(公式一).难点:任意角的正弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号);三角函数线的正确理解.【学法指导】1.了解三角函数的两种定义方法;2.知道三角函数线的基本做法.【知识链接】:根据课本本节内容,完成预习目标,完成以下各个概念的填空.三、提出疑惑同学们,通过你的自主学习,你还有哪些疑惑,请把它填在下面的表格中疑惑点疑惑内容【学习过程】(一)复习:1、初中锐角的三角函数______________________________________________________2、在Rt△ABC中,设A对边为a,B对边为b,C对边为c,锐角A的正弦、余弦、正切依次为_______________________________________________(二)新课:1.三角函数定义在直角坐标系中,设α是一个任意角,α终边上任意一点(除了原点)的坐标为,它与原点的距离为,那么(1)比值_______叫做α的正弦,记作_______,即________(2)比值_______叫做α的余弦,记作_______,即_________(3)比值_______叫做α的正切,记作_______,即_________;2.三角函数的定义域、值域函数定义域值域[来源:学科网]3.三角函数的符号由三角函数的定义,以及各象限内点的坐标的符号,我们可以得知:①正弦值对于第一、二象限为_____(),对于第三、四象限为____();②余弦值对于第一、四象限为_____(),对于第二、三象限为____();③正切值对于第一、三象限为_______(同号),对于第二、四象限为______(异号).4.诱导公式由三角函数的定义,就可知道:__________________________即有:___________________________________________________________________________5.当角的终边上一点的坐标满足_______________时,有三角函数正弦、余弦、正切值的几何表示——三角函数线。设任意角的顶点在原点,始边与轴非...