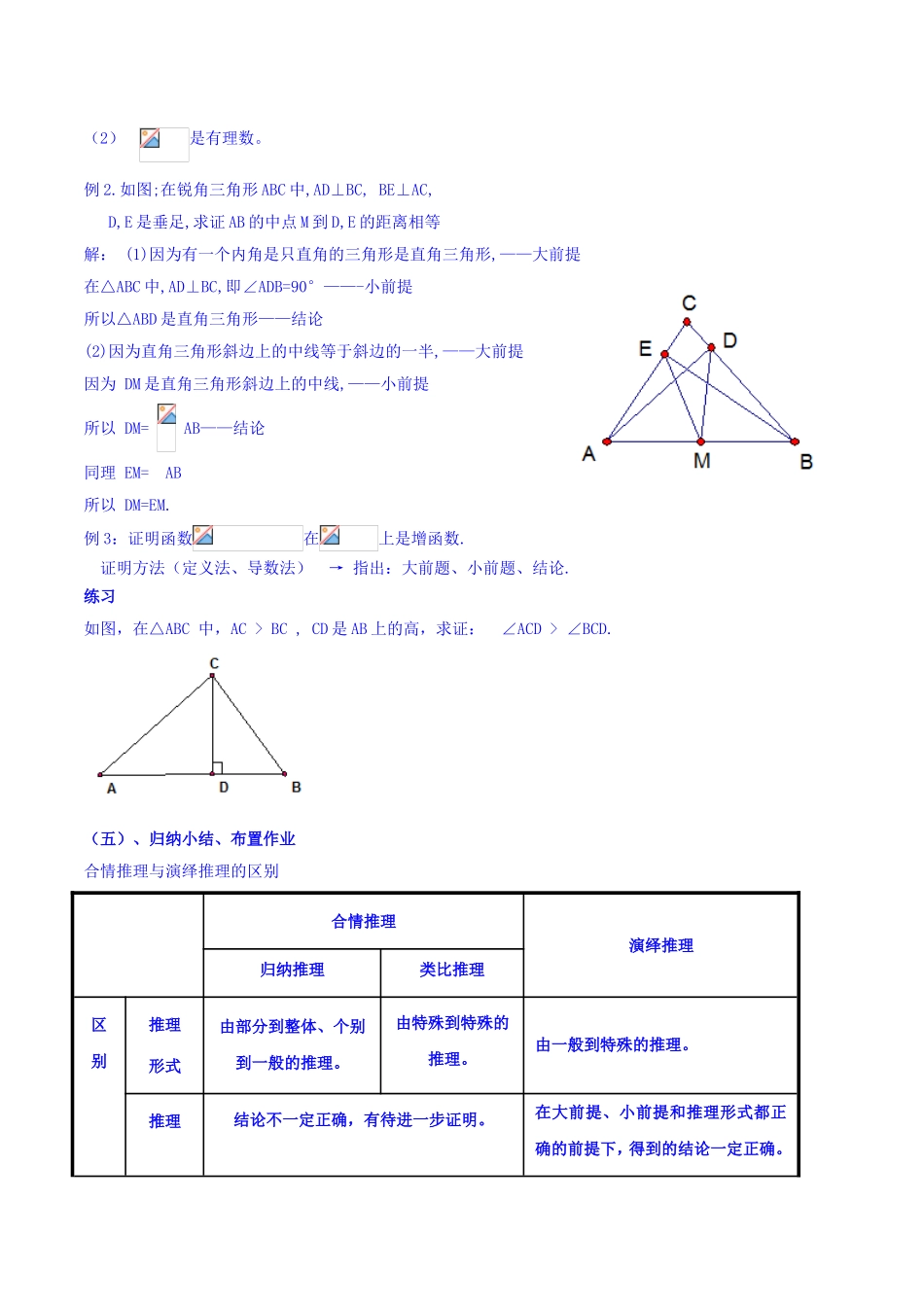
§2.1.2演绎推理教学目标:1.了解演绎推理的含义。2.能正确地运用演绎推理进行简单的推理。3.了解合情推理与演绎推理之间的联系与差别。教学重点:正确地运用演绎推理进行简单的推理;教学难点:了解合情推理与演绎推理之间的联系与差别.教学过程设计(一)、复习引入,激发兴趣。【教师引入】复习:合情推理归纳推理从特殊到一般类比推理从特殊到特殊从具体问题出发――观察、分析比较、联想――归纳。类比――提出猜想合情推理的结论不一定正确,有待进一步证明,有什么能使结论正确的推理形式呢?(二)、探究新知,揭示概念①所有的金属都能够导电,铜是金属,所以;②太阳系的大行星都以椭圆形轨道绕太阳运行,冥王星是太阳系的大行星,因此;③奇数都不能被2整除,2017是奇数,所以.(填空→讨论:上述例子的推理形式与我们学过的合情推理一样吗?(三)、分析归纳,抽象概括从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理。要点:由一般到特殊的推理。“三段论”是演绎推理的一般模式:第一段:大前提——已知的一般原理;第二段:小前提——所研究的特殊情况;第三段:结论——根据一般原理,对特殊情况做出的判断.三段论的基本格式M—P(M是P)(大前提)S—M(S是M)(小前提)S—P(S是P)(结论)3.三段论推理的依据,用集合的观点来理解:若集合M的所有元素都具有性质P,S是M的一个子集,那么S中所有元素也都具有性质P.(四)、知识应用,深化理解例1:用三段论的形式写出下列演绎推理。(1)三角形内角和180°,等边三角形内角和是180°.(2)是有理数。例2.如图;在锐角三角形ABC中,AD⊥BC,BE⊥AC,D,E是垂足,求证AB的中点M到D,E的距离相等解:(1)因为有一个内角是只直角的三角形是直角三角形,——大前提在△ABC中,AD⊥BC,即∠ADB=90°——-小前提所以△ABD是直角三角形——结论(2)因为直角三角形斜边上的中线等于斜边的一半,——大前提因为DM是直角三角形斜边上的中线,——小前提所以DM=AB——结论同理EM=AB所以DM=EM.例3:证明函数在上是增函数.证明方法(定义法、导数法)→指出:大前题、小前题、结论.练习如图,在△ABC中,AC>BC,CD是AB上的高,求证:∠ACD>∠BCD.(五)、归纳小结、布置作业合情推理与演绎推理的区别合情推理演绎推理归纳推理类比推理区别推理形式由部分到整体、个别到一般的推理。由特殊到特殊的推理。由一般到特殊的推理。推理结论不一定正确,有待进一步证明。在大前提、小前提和推理...