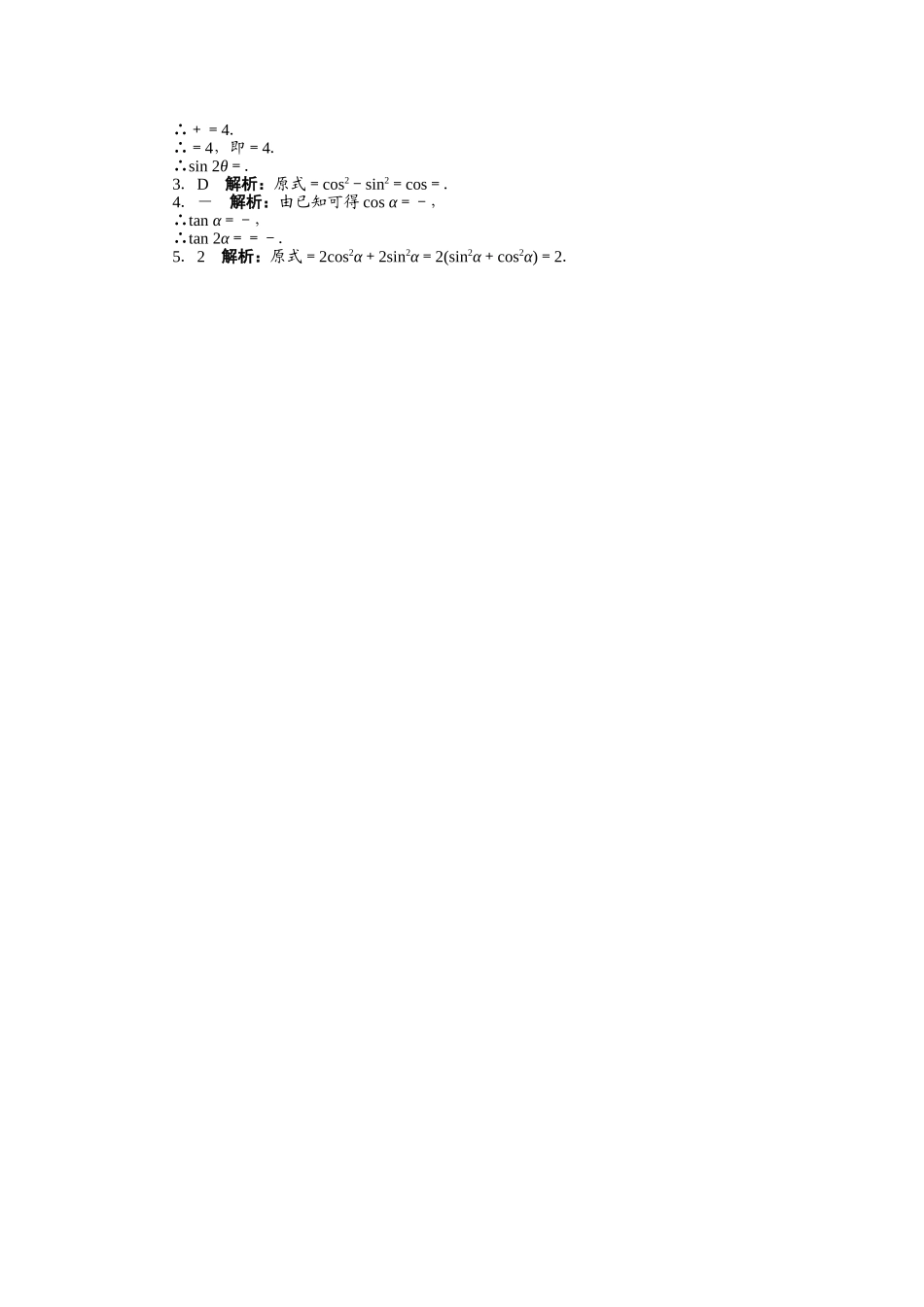
3.1.3二倍角的正弦、余弦、正切公式问题导学一、给角求值活动与探究1求下列各式的值:(1)2cos2-1;(2);(3)-;(4)cos20°cos40°cos80°.迁移与应用1.求下列各式的值:(1)cos215°-sin215°;(2)coscosπ.2.求+的值.解答此类题目一方面要注意角的倍数关系,另一方面要注意函数名称的转化方法,同角三角函数的关系及诱导公式是常用方法.二、给值化简求值问题活动与探究2已知sin=,0<x<,求的值.迁移与应用(1)已知cos=,则sin2x=()A.B.C.-D.-(2)已知tanα=-,则=________.(1)从角的关系寻找突破口.这类三角函数求值问题常有两种解题途径:一是对题设条件变形,将题设条件中的角、函数名向结论中的角、函数名靠拢;另一种是对结论变形,将结论中的角、函数名向题设条件中的角、函数名靠拢,以便将题设条件代入结论.(2)另外,注意几种诱导公式的应用,如:①sin2x=cos=cos=2cos2-1=1-2sin2;②cos2x=sin=sin=2sincos;③cos2x=sin=sin=2sincos.三、关于三角函数式的证明问题活动与探究3求证:=sin2α.迁移与应用求证:=tan4A.当堂检测1.sin15°cos15°的值等于()A.B.C.D.2.若tanθ+=4,则sin2θ=()A.B.C.D.3.的值为()A.-B.-C.D.4.已知α∈,sinα=,则tan2α=________.5.化简1+cos2α+2sin2α=__________.提示:用最精炼的语言把你当堂掌握的核心知识的精华部分和基本技能的要领部分写下来并进行识记。答案:课前预习导学【预习导引】2sinαcosαcos2α-sin2α2cos2α-11-2sin2α预习交流1提示:在两角和的正弦、余弦、正切公式中,令β=α即可得到.常用的变形有:cos2α=,sin2α=等.预习交流2提示:公式S2α,C2α中,角α可以为任意角;但公式T2α只有当α≠+kπ且α≠+(k∈Z)时才成立,否则不成立(因为当α=+kπ,k∈Z时,tanα的值不存在;当α=+,k∈Z时,tan2α的值不存在).当α=+kπ,k∈Z时,虽然tanα的值不存在,但tan2α的值是存在的,这时求tan2α的值可利用诱导公式,即tan2α=tan2=tan(π+2kπ)=tanπ=0.课堂合作探究【问题导学】活动与探究1思路分析:可以利用二倍角公式及其相关变形求解.解:(1)原式=cos=cos=cos=.(2)原式==2×=2×=2.(3)原式=====4.(4)原式=====.迁移与应用1.解:(1)原式=cos(2×15°)=cos30°=.(2)原式=cossin=sin=.2.解:原式=====4.活动与探究2思路分析:解答本题可...