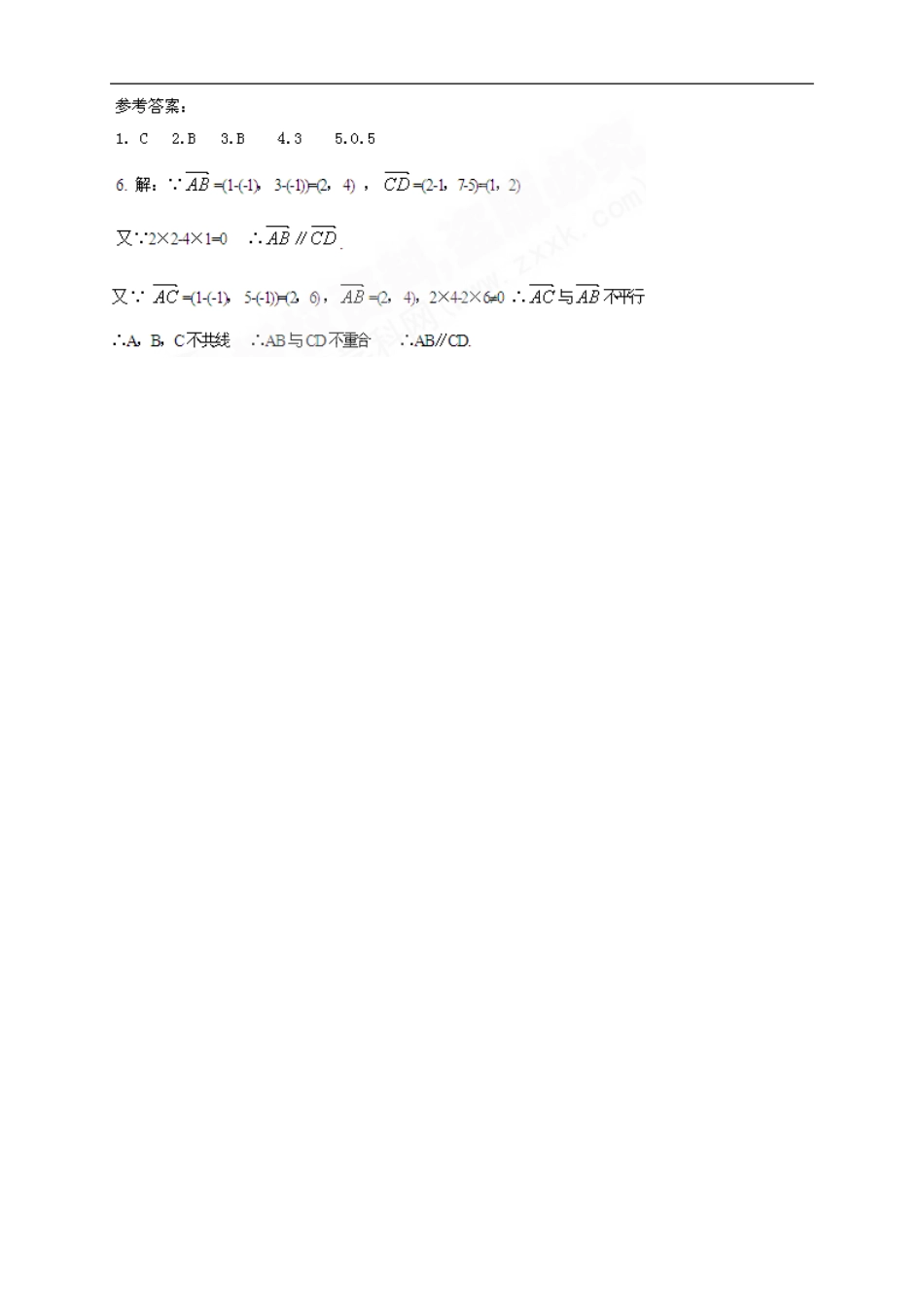
2.3.4《平面向量共线的坐标表示》导学案【学习目标】:1.会推导并熟记两向量共线时坐标表示的充要条件;2.能利用两向量共线的坐标表示解决有关综合问题。3.通过学习向量共线的坐标表示,使学生认识事物之间的相互联系,培养学生辨证思维能力.【学法指导】通过预习会初步利用两向量共线时坐标表示的充要条件进行预算.【知识链接】:1、知识回顾:平面向量共线定理________________________________________.[来源:学§科§网]2.平面向量共线的坐标表示:设=(x1,y1)=(x2,y2)(¹)其中¹,则∥(¹)_____________________.三、提出疑惑同学们,通过你的自主学习,你还有哪些疑惑,请把它填在下面的表格中[来源:学科网ZXXK]疑惑点疑惑内容【学习过程】1.思考:共线向量的条件是当且仅当有一个实数λ使得=λ,那么这个条件是否也能用坐标来表示呢?设=(x1,y1),=(x2,y2)(¹)其中¹由=λ,得___________________,即__________________________,消去λ后得:__________________________________.这就是说,当且仅当___________________时,向量与共线.2.典型例题例1已知,,且,求.[来源:Z*xx*k.Com]例2:已知,,,求证、、三点共线.例3:设点P是线段P1P2上的一点,P1、P2的坐标分别是(x1,y1),(x2,y2).(1)当点P是线段P1P2的中点时,求点P的坐标;(2)当点P是线段P1P2的一个三等分点时,求点P的坐标.[来源:学科网]【学习反思】1.平面向量共线充要条件的两种表达形式是什么?2.如何用平面向量共线的充要条件的坐标形式证明三点共线和两直线平行?3.判断两直线平行与两向量平行有什么异同?【基础达标】1.已知=+5,=-2+8,=3(-),则()A.A、B、D三点共线B.A、B、C三点共线[来源:学&科&网Z&X&X&K]C.B、C、D三点共线D.A、C、D三点共线2.若向量=(-1,x)与=(-x,2)共线且方向相同,则x为________.3.设,,,且,求角.【拓展提升】1.若=(2,3),=(4,-1+y),且∥,则y=()A.6B.5C.7D.82.若A(x,-1),B(1,3),C(2,5)三点共线,则x的值为()A.-3B.-1C.1D.33.若=i+2j,=(3-x)i+(4-y)j(其中i、j的方向分别与x、y轴正方向相同且为单位向量).与共线,则x、y的值可能分别为()A.1,2B.2,2C.3,2D.2,44.已知=(4,2),=(6,y),且∥,则y=.5.已知=(1,2),=(x,1),若+2与2-平行,则x的值为6.已知A(-1,-1),B(1,3),C(1,5),D(2,7),向量与平行吗?直线AB与平行于直线CD吗?