3.1.3导数的几何意义.docVIP免费

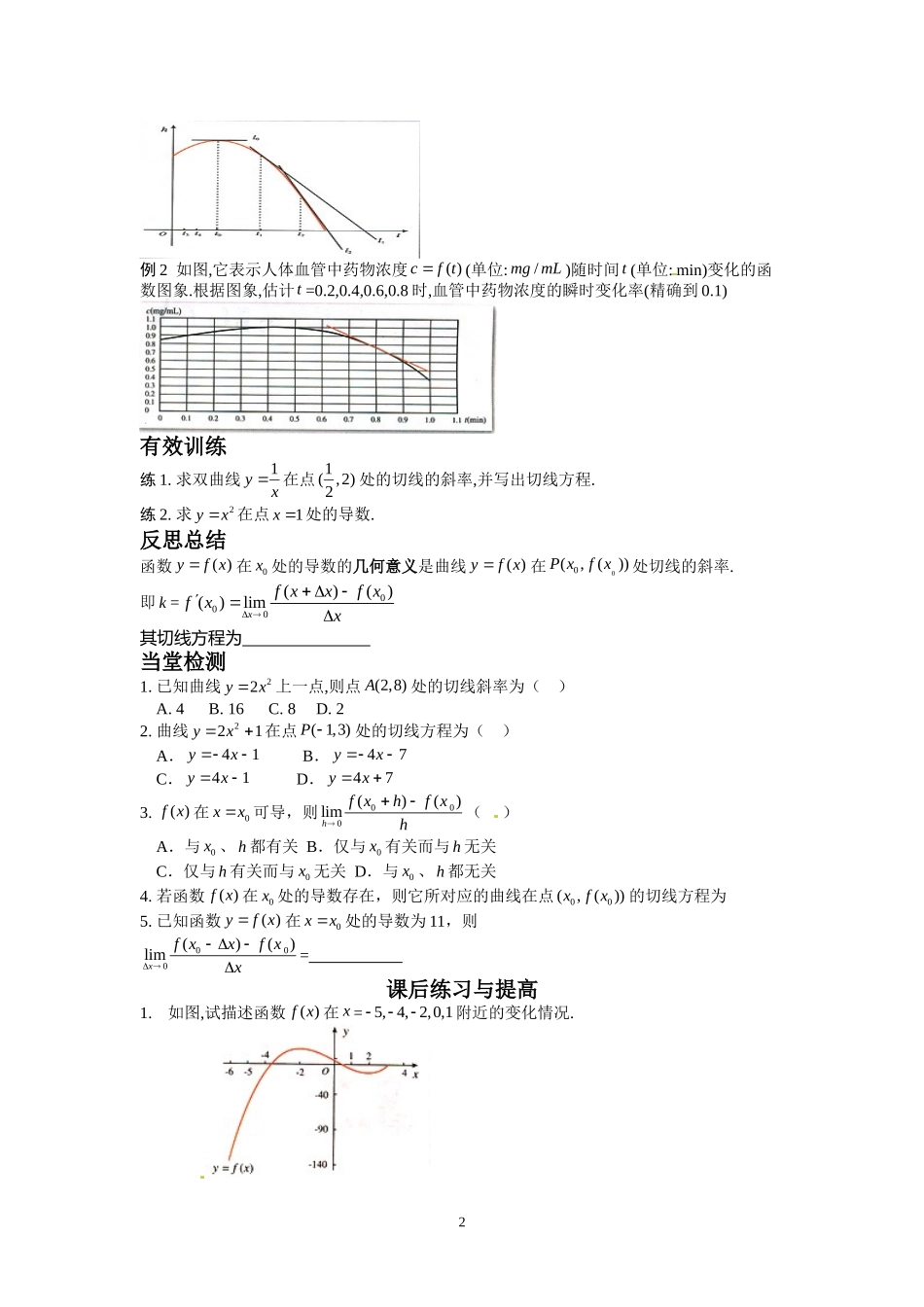
导数的几何意义课前预习学案预习目标：导数的几何意义是什么？（预习教材P78~P80，找出疑惑之处）复习1：曲线上向上11111(,),(,)PxyPxxyy的连线称为曲线的割线，斜率ykx复习2：设函数()yfx在0x附近有定义当自变量在0xx附近改变x时，函数值也相应地改变y，如果当x时，平均变化率趋近于一个常数l，则数l称为函数()fx在点0x的瞬时变化率.记作：当x时，l上课学案学习目标：通过导数的图形变换理解导数的几何意义就是曲线在该点的切线的斜率，知道导数的概念并会运用概念求导数.学习重难点：导数的几何意义学习过程：学习探究探究任务：导数的几何意义问题1：当点(,())(1,2,3,4)nnnPxfxn，沿着曲线()fx趋近于点00(,())Pxfx时，割线的变化趋是什么？新知：当割线PnP无限地趋近于某一极限位置PT奎屯王新敞新疆我们就把极限位置上的直线PT，叫做曲线C在点P处的切线奎屯王新敞新疆割线的斜率是：nk当点nP无限趋近于点P时，nk无限趋近于切线PT的斜率.因此，函数()fx在0xx处的导数就是切线PT的斜率k，即0000()()lim()xfxxfxkfxx新知：函数()yfx在0x处的导数的几何意义是曲线()yfx在00(,())Pxfx处切线的斜率.即k=000()()()limxfxxfxfxx典型例题例1如图,它表示跳水运动中高度随时间变化的函数2()4.96.510httt的图象.根据图象,请描述、比较曲线()ht在012,,ttt附近的变化情况.1例2如图,它表示人体血管中药物浓度()cft(单位:/mgmL)随时间t(单位:min)变化的函数图象.根据图象,估计t=0.2,0.4,0.6,0.8时,血管中药物浓度的瞬时变化率(精确到0.1)有效训练练1.求双曲线1yx在点1(,2)2处的切线的斜率,并写出切线方程.练2.求2yx在点1x处的导数.反思总结函数()yfx在0x处的导数的几何意义是曲线()yfx在00(,())Pxfx处切线的斜率.即k=000()()()limxfxxfxfxx其切线方程为当堂检测1.已知曲线22yx上一点,则点(2,8)A处的切线斜率为（）A.4B.16C.8D.22.曲线221yx在点(1,3)P处的切线方程为（）A．41yxB．47yxC．41yxD．47yx3.()fx在0xx可导，则000()()limhfxhfxh（）A．与0x、h都有关B．仅与0x有关而与h无关C．仅与h有关而与0x无关D．与0x、h都无关4.若函数()fx在0x处的导数存在，则它所对应的曲线在点00(,())xfx的切线方程为5.已知函数()yfx在0xx处的导数为11，则000()()limxfxxfxx=课后练习与提高1.如图,试...